Окончательно получаем

.

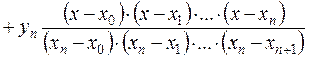Этот многочлен называется интерполяционным многочленом Лагранжа

,

где х₀, х₁,…. х_n – узлы интерполяции, а х – значение аргумента, для которого определяется приближенное значение по интерполяционной формуле Лагранжа.

Обозначим произведение элементов первой строки через R₀:

.

В общем виде произведение элементов i строки

.

Дополнительно вычислим произведение элементов, расположенных на главной диагонали

,

тогда интерполяционный многочлен Лагранжа можно переписать в виде

.

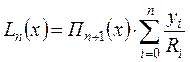Интерполяционная формула Лагранжа заметно упрощается, если узлы интерполяции равноотстоящие, т.е. .

Обозначим q = (x - x₀)/h , тогда

.

Введем обозначения:

…

,

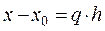
тогда

.

Заметим, что часть произведения в знаменателе равна

,

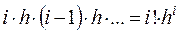а другая

.

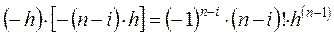Умножив числитель и знаменатель правой части последнего равенства на (-1)^n-i(q - i), получим

,

где

.

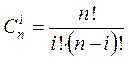Интерполяционный многочлен Лагранжа для равноотстоящих узлов интерполяции теперь можно записать в виде

.