Матричные уравнения

Рассмотрим три вида матричных уравнений.

1. Уравнение вида 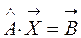. Умножим обе части уравнения на 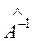слева:

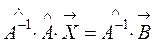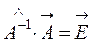, где . (1.7)

Пример: 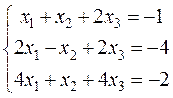или .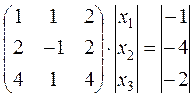

Находим обратную матрицу 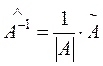. 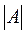- детерминант матрицы A.

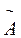- алгебраическое дополнение к матрице A.

; .

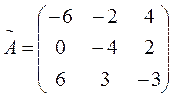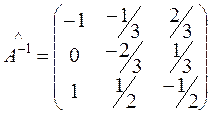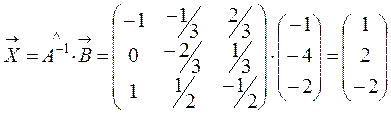
2. Матричное уравнение вида:

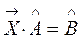(1.8)

Умножим обе части уравнения на 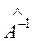справа.

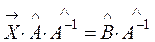
Пример:Решить матричное уравнение

.

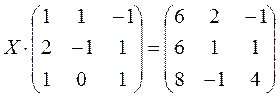Решение:

~ ; ;

; ; ;

; ; ;

; ; ;

; ;

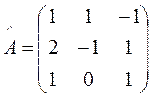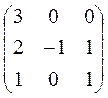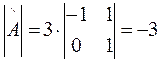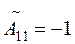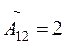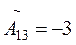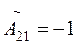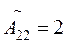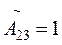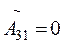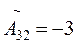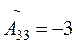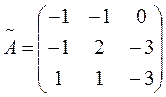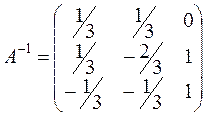Матричное уравнение третьего вида:

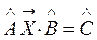. (1.9)

Для его решения умножим обе части уравнения слева на 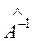, а справа на 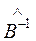, тогда получим

;

.

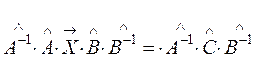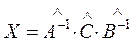Пример:Решить матричное уравнение

.

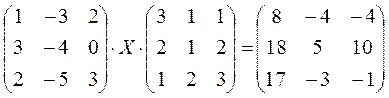Решение:

; ; ;

; ; ;

.

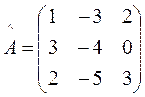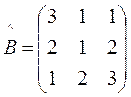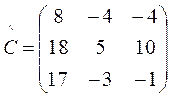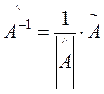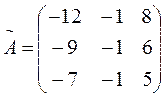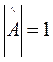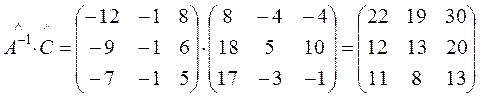Находим сначала 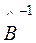, а затем и искомое решение матричного уравнения

; ; ;

.

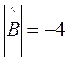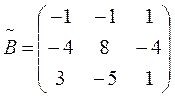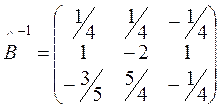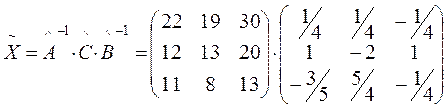ЛЕКЦИЯ 2. ТОЧНЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ)

СЛАУ допускают как точные, так и приближенные методы решения.

К точным относятся метод Крамера, метод Гаусса и метод обратной матрицы.

К приближенным методам относятся: метод простой итерации, метод последовательных приближений и метод Зейделя.