Абсолютные и относительные погрешности

Источники погрешностей

1. Неточное отображение реальных процессов с помощью математики, когда рассматривается не сам процесс, а его математическая идеализация. Поэтому не всегда реальные условия могут быть хорошо описаны математически.

2. Приближенные значения величин, входящих в условия задачи (погрешности исходных данных).

3. Замена бесконечных процессов, пределами которых являются искомые величины, конечной последовательностью действий.

4. Округление исходных данных, промежуточных или окончательных результатов из-за малой разрядности машины.

5. Кроме указанных выше случаев, погрешности могут появляться в результате действий над приближенными числами. Полная погрешность является результатом сложного взаимодействия всех видов погрешности. При решении конкретных задач те или иные погрешности могут отсутствовать или мало влиять на образование полной погрешности. Однако для полного анализа необходимо учитывать все их виды.

Погрешности можно подразделить на три большие группы:

1. Исходные (или неустранимые) погрешности, к которым относятся погрешности, возникающие в результате приближенного описания реальных процессов и неточного задания исходных данных. Эти погрешности проходят через все вычисления и являются неустранимыми.

2. Погрешности округления, которые появляются в результате округления исходных данных, промежуточных и окончательных результатов.

3. Остаточные погрешности возникают в результате замены бесконечных процессов конечной последовательностью действий.

Оценка погрешности может быть произведена с помощью абсолютной погрешности, с помощью относительной погрешности, с помощью остаточного члена, с помощью статических оценок.

При работе с приближенными величинами, вычислитель должен уметь:

- давать математические характеристики точности приближенных величин;

- зная степень точности исходных данных, оценивать степень точности результатов;

- брать исходные данные с такой степенью точности, чтобы обеспечить заданную точность результата;

- правильно организовать вычислительный процесс, чтобы избавить его от тех выкладок, которые не окажут влияния на точные цифры результатов.

Абсолютные и относительные погрешности

Принципиальная трудность работы с вещественными числами заключается в том, что любая переменная в памяти ЭВМ может принимать лишь конечное число значений, поэтому вещественные числа не могут быть представлены в компьютере точно. Числа записываются в форме с плавающей запятой.

При этом отдельно хранится мантисса М. Число М по абсолютной величине не превосходит 1 и порядок P, значит, пара (Р,М) задает вещественное число

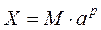
В ЭВМ, как правило, а = 2 или a = 16. Для записи мантиссы используется фиксированное число k, т.е.

,

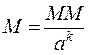где ММ – целое число и

.

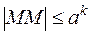Диапазон изменения порядка тоже ограничен:

.

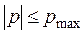Значит, представление чисел в компьютере обладает следующими свойствами:

1. Абсолютная погрешность равна абсолютной величине разности точного числа и приближенного .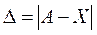

2. Относительная погрешность равна отношению абсолютной погрешности к точным значениям .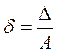

3. Невозможно представить очень большие по модулю и очень малые («нулевые») числа. Произвольное вещественное число, попадающее в допустимый интервал, может быть написано с некоторой погрешностью. Относительная погрешность в этом случае примерно постоянна и равна .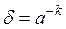

Рассмотрим ошибки вычислений, связанных с вычитанием близких чисел – действие, приводящее к потере точности

,

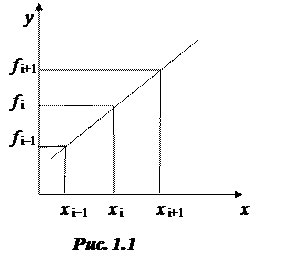
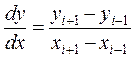или

.

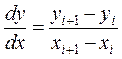Следующий источник ошибок – суммирование слагаемых с различным порядком сложения:

55,55 + 0,001 + 0,001 + … + 0,001 .

Мы не можем хранить пятую цифру, т.е. результат будет 55,55, следовательно, останется без изменений. А если сначала сложить 100 х 0,001 = 0,1 получим 55,61. Поэтому суммирование чисел необходимо производить в порядке возрастания слагаемых.