Приведение системы линейных уравнений к виду, удобному для итераций

Процессы последовательных приближений и метод Зейделя для линейных систем х = b + aC сходятся к единому решению, независимо от выбора начального вектора, если

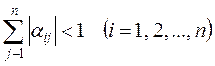
или

.

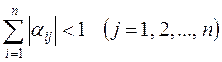Таким образом, для сходимости вышеуказанных итерационных процессов достаточно, чтобы значения элементов a_ij при i ¹ j были небольшими по абсолютной величине. Это равносильно тому, что если для линейной системы АХ = В модули диагональных коэффициентов каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов), то итерационные процессы для этой системы сходятся, т.е. мы имеем систему

.

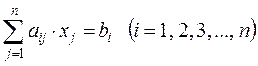Причем, если 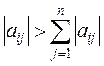то процессы последовательных приближений и Зейделя для данной системы сходятся. Применяя элементарные преобразования, линейную систему АХ = В можно заменить такой эквивалентной системой Х = р + aХ, для которой условия сходимости будут выполнены.

ЛЕКЦИЯ 5. МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

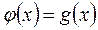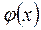При решении практических задач, часто приходится сталкиваться с решением уравнений. Всякое уравнение с одним неизвестным можно представить в виде , где и 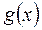– заданные функции, определенные на некотором числовом множестве Х, называемом областью допустимых значений уравнения или

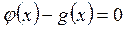
если обозначить левую часть за 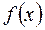, то получим уравнение .

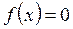Совокупность нескольких уравнений с несколькими неизвестными называют системой уравнений.