Понятие о системе линейных уравнений
В общем виде система m линейных уравнений с n неизвестными записывается так:
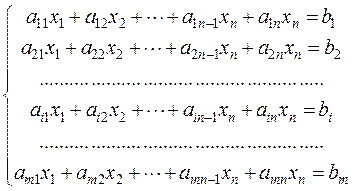 (1.1)
(1.1)
Уравнения системы считаются пронумерованными: первое, второе, 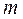 - е,
- е, 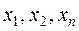 – неизвестные,
– неизвестные, 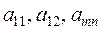 – коэффициенты при неизвестных.
– коэффициенты при неизвестных.
Коэффициент при неизвестном 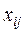 в i – уравнении обозначается через
в i – уравнении обозначается через 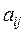 , j – номер неизвестного.
, j – номер неизвестного.
Кратко система (1.1) может быть записана:
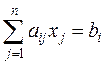 , (i = 1, 2, …, m). (1.2)
, (i = 1, 2, …, m). (1.2)
Решением системы линейных уравнений называется любая совокупность чисел 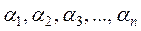 , которая, будучи подставленной на место неизвестных
, которая, будучи подставленной на место неизвестных 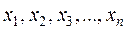 в уравнение данной системы, обращает все эти уравнения в тождества. Система (1.1) – совместная, если она имеет решение. Если система не имеет решений, то она называется несовместной или противоречивой.
в уравнение данной системы, обращает все эти уравнения в тождества. Система (1.1) – совместная, если она имеет решение. Если система не имеет решений, то она называется несовместной или противоречивой.
Совместная система линейных уравнений может иметь одно или несколько решений. Она называется определенной, если имеет одно решение, и неопределенной, если имеет больше одного решения.
Две системы линейных уравнений с одним и тем же числом неизвестных называются эквивалентными, если они обе несовместны или совместны и имеют одни и те же решения.
Пусть дана определенная система n линейных уравнений (1.1). Пользуясь матричными обозначениями её, можно заменить следующим:
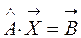 , (1.3)
, (1.3)
где матрица системы
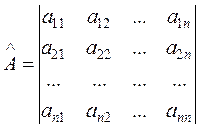 ; (1.4)
; (1.4)
вектор-столбец неизвестных
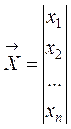 ; (1.5)
; (1.5)
вектор-столбец свободных членов
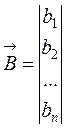 . (1.6)
. (1.6)
Дата добавления: 2021-09-07; просмотров: 491;











