Пусть дана линейная система
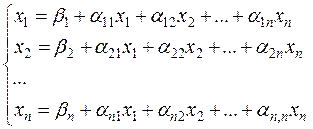 (4.1)
(4.1)
Выбираем произвольно начальное приближение корней 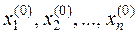 и подставляем в первое уравнение системы (4.1)
и подставляем в первое уравнение системы (4.1)
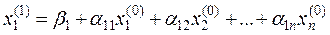 ,
,
полученное первое приближение подставляем во второе:
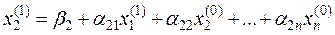 .
.
Полученные первые приближения х1(1) и х2(1) подставляем в третье уравнение системы (4.1)
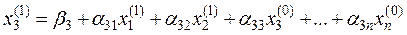
и т. д.
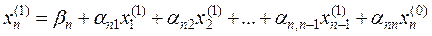 .
.
Аналогично строим вторые и третьи итерации.
Таким образом, предполагая, что k приближение корней хki известно, по методу Зейделя строим (k + 1) приближение
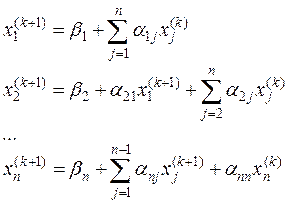
где k = 0, 1, 2, …, n.
Пример. Методом Зейделя решим систему:
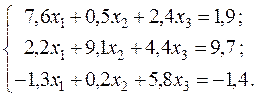
1. Приведем систему к нормальному виду:
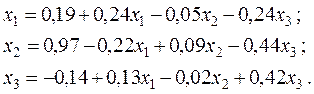
2. За нулевые значения возьмем соответствующие значения свободных членов
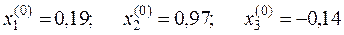 .
.
3. Строим итерации по методу Зейделя
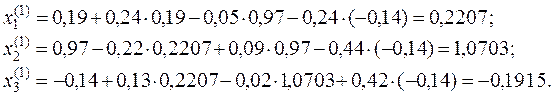
Второе приближение
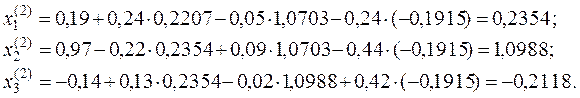
И т.д.
| №итерации | 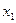
| 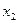
| 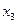
|
| 0,19 | 0,97 | -0,14 | |
| 0,2207 | 1,0703 | -0,1915 | |
| 0,2354 | 1,0988 | -0,2118 | |
| 0,2424 | 1,1088 | -0,2196 | |
| 0,2454 | 1,1124 | -0,2226 | |
| 0,2467 | 1,1138 | -0,2237 | |
| 0,2472 | 1,1143 | -0,2241 | |
| 0,2474 | 1,1145 | -0,2243 | |
| 0,2475 | 1,1145 | -0,2243 |
Построенный процесс заканчивается, когда с заданной степенью точности получаем одинаковые значения в двух итерациях подряд.
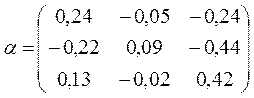 ;
; 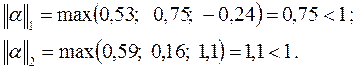
Процесс Зейделя для линейной системы Х = b + aХ также, так и процесс последовательных приближений, сходится к единственному решению при любом выборе начального приближения, если какая-нибудь из норм матрицы a меньше единицы. То есть
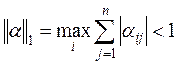
либо
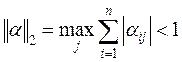 ,
,
либо
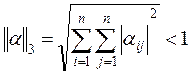 .
.
Процесс Зейделя сходится к единственному решению быстрее процесса простой итерации.
Дата добавления: 2021-09-07; просмотров: 567;











