Оценка погрешности приближенного процесса методом итерации

Если задана допустимая погрешность вычислений 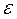и Х_i – вектор точных значений неизвестных линейной системы, а Х_i^(k) – есть k приближение значений неизвестных, вычисленное методом итераций, то для оценки погрешности || Х_i - Х_i^(k)|| £ 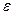метода применяется формула

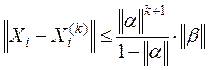. (3.8)

где ||a|| – одна из трех норм матрицы a, ||b|| – та же норма вектора b, а k – число итераций, необходимое для достижения заданной точности.

При этом предполагается, что последовательное приближение Х_i^(j) (где j = 0, 1, 2, 3, …, k; i = 1, 2, …, n) вычисляется точно, в нем отсутствуют погрешности округления.

Пример. Методом последовательного приближения решить систему

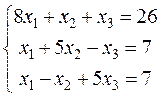
1. Приведем данную систему к нормальному виду

; .

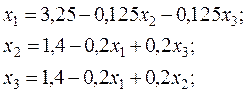
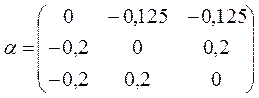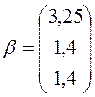2. Строим последовательные приближения.

Нулевое:

.

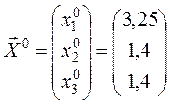Первое:

.

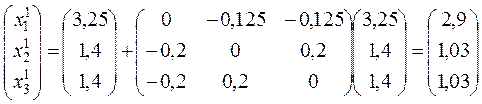Второе:

.

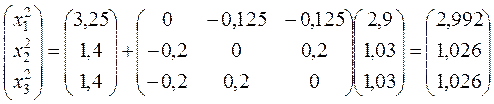Третье:

.

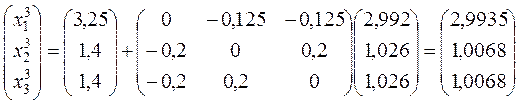С точностью 10^-1 получаем х₁ = 3, х₂ = 1, х₃ = 1.

Итерационный процесс сходится, т.к.

;

.

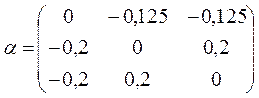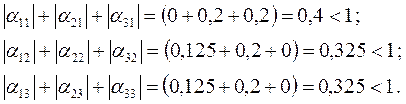Процесс итераций заведомо сходится, если элементы матрицы a удовлетворяют неравенству |a_ij| < 1/n, где n - число неизвестных данной системы.

В нашем примере n = 3, |a_ji| < 1/3. Используя норму ,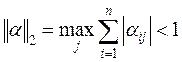

||a||₂ = max (0,4; 0,325; 0,325)=0,421 .

Соответствующая матрица ||b||₂ = (3,25 + 1,4 + 1,4) = 6,05 .

Применяя формулу

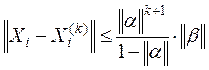
при ε =10^-4 , получим

.

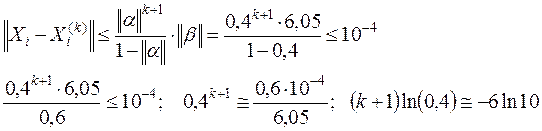или 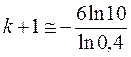, значит 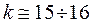итераций.

ЛЕКЦИЯ 4. МЕТОД ЗЕЙДЕЛЯ