Примеры, имеющие самостоятельное значение

1. 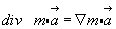(3.24)

(операция дивергенции, примененная к произведению скаляра на вектор, каждый из которых есть переменная величина).

В соответствии с правилами производная от произведения равна сумме производных, т.е.

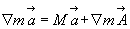(3.25)

здесь малые буквы ( m и 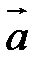) обозначают переменные величины, а большие буквы (M и 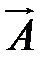) – величины, которые временно рассматриваются как постоянно.

Вынесем скаляр M за знак (дифф-я), а во втором слагаемом оператор (Гамильтона) будем рассматривать как обычный вектор. Тогда 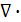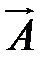есть просто скалярное произведение двух векторов, величина которого не меняется от перестановки сомножителей.

Значит, в процессе преобразования 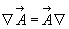и постоянный вектор 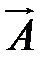оказался как бы вынесенным за знак производной.

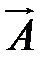
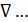Т.о. в результате такого преобразования получили новый оператор дифференцирования ( )… , который в отличие от является скалярным, а не векторным.

Примечание:

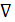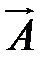
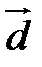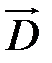
Для преобразования членов ( ) и ( 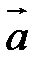) необходимо искать формулы в векторной алгебре, которые включали бы комплексы типа ( ∙ ).

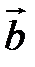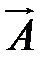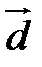Оказывается, что такой комплекс есть в разложении двойного векторного произведения: ( ∙ ) = ( + ( ∙ ) .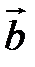

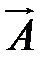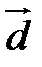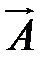
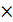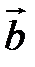
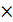
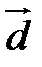
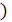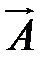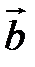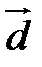После проведения преобразований величины, принятые временно как постоянные, будем (можно) снова считать переменными.

Т.о. равенство (3.25) можно записать:

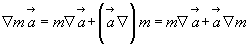(3.26)

Замечание:

Т.к. после введения нами нового оператора дифференцирования ( 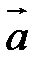)… стоит переменная скалярная величина, то скобки, охватывающие этот оператор, можно не ставить.

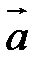
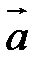
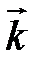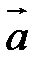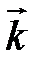
Если бы за знаком ( )… следовал вектор, то они (скобки) были бы обязательны. В противном случае выражение , и так: ( 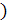, а про правилам действия над векторами .

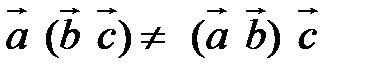Т.о. окончательно выражение (3.26) можно записать:

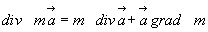(3.27)

2. Найдем выражение для grad ( 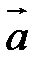∙ 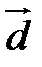), где 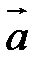и 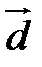переменные векторы.

первый шаг: запишем:

(*)

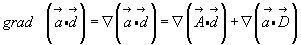Здесь мы не имеем права, как в предыдущем примере, делать преобразования вида:

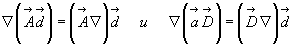
т.к. знаки равенства в этих выражениях незаконны из-за справедливости .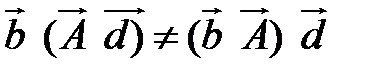

Из векторной алгебры известно:

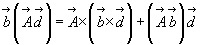
Т.о. заменив в этом отношении вектор 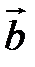на оператор Гамильтона , получим для первого слагаемого равенства (*) такое выражение:

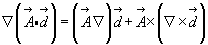
Аналогично представляется и второе слагаемое (*):

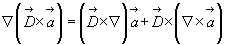
Наконец, считая все векторы вновь переменными, запишем следующую зависимость:

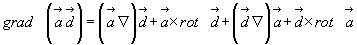(3.28)

Замечание 1:

В дальнейшем нас будет интересовать лишь частный случай этой формулы, когда оба вектора 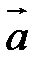и 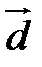равны вектору скорости.

Т.о из выр-я (3.28) автоматически получаем:

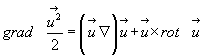(3.29)

Замечание 2:

Введенные нами величины ( )… и … являются дифференциальными операторами первого порядка, причем один из этих операторов векторный, а другой – скалярный. Они как бы символизируют первую производную от функции пространственных переменных.

Примечание:

Рассмотренные рассуждения о лапласиане, дивергенции, градиенте и т.д. (полезно) необходимо помнить при чтении основных уравнению гидродинамики. Тогда, записанные в символах векторного анализа, они (эти уравнения) приобретают свойственную им физическую простоту и ясность.