III. ОПЕРАТОРЫ И НАБЛЮДАЕМЫЕ

Операторы

& Литература: [8], [3], [1], [7].

Во всех физических уравнениях присутствуют некоторые математические действия, производимые над величинами, характеризующими состояния описываемых объектов. Действия над математическими объектами, а также символы этих действий называют операторами. Аналогично и в уравнениях квантовой механики фигурируют операторы. Они предполагают действия над квантово-механическими векторами состояний или над амплитудами состояний, а не только над функциями и числами.

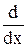В квантовой механике за редким исключением символ оператора ставится перед тем математическим объектом, на который направлено действие оператора: úYñ = újñ; Y(x) = j(x). Примеры исключений: Y* = j;
Y² = j и др.

Оператор называют линейным, если для любых ú j₁ñ и ÷j₂ñ, а также произвольных комплексных чисел a₁ и a₂ выполняется условие:

(ú j₁ñ a₁+ új₂ñ a₂) = ú j₁ñ a₁+ ú j₂ñ a₂. (8.1)

Здесь и далее записываются соотношения для операторов, действующих на векторы состояний. Аналогичные соотношения и свойства относятся и к операторам, действующим на волновые функции. В этом случае под символом újñ следует понимать соответствующую функцию j. В квантовой механике используются только линейные операторы, поскольку их применение к векторам состояния не нарушает принцип суперпозиции: все полученные векторы, как и исходные, могут быть представлены линейной комбинацией других.

Оператор считают равным нулю, если его действие на любой вектор дает нуль-вектор 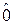újñ = ú0ñ. Нуль-вектор определяется равенством:

újñ + ú0ñ = újñ.

Единичный оператор оставляет без изменения произвольный вектор: 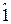újñ = újñ. Примером единичного оператора может служить выражение 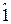= 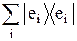, поскольку в случае полного базиса úe_iñ любой вектор ÷Añ можно представить в виде: ÷Añ = 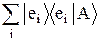. Поэтому равенство 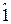= 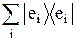является условием полноты базиса.

Равными называют операторы = , применение которых к произвольному вектору приводит к одинаковым результатам: равенство újñ= újñ должно выполняться для любого újñ.

Аналогично алгебре чисел и функций построена и алгебра операторов.

Под суммой операторов и понимают оператор + , если для любого újñ имеет место равенство ( + )újñ = újñ + újñ. Подобно этому для произведения операторов должно выполняться соотношение ( )újñ = ( újñ). Сумма операторов коммутативна, а произведение, вообще говоря, нет: ¹ . Если же операторы коммутируют, то для них – = 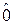. Оператор [ ] = – называют коммутатором. Если коммутатор операторов равен нулю, то эти операторы коммутируют.

Все определения и соотношения для операторов , действующих в cket-пространстве, переносятся и на операторы ⁺, действующие в сопряженном пространстве. Если újñ = úY1ñ, то ájï ⁺ú= áY1ï. Оператор ⁺ называют оператором, сопряженным оператору . Для сопряженного оператора справедливо равенство ájï ⁺úYñ = áYï újñ*. (8.2)

Можно показать, что

( + )⁺ = ⁺ + ⁺ и что ( )⁺ = ^{+ +}. (8.3)

Оператор , для которого выполняется соотношение

ájï úYñ = áYï újñ* , или ájï úYñ = ájï ⁺úYñ, (8.4)

называют самосопряженным, или эрмитовым. Если поменять обкладки эрмитова оператора, то получается комплексно сопряженная величина. Последнее равенство кратко записывают в виде = ⁺. Не следует при этом забывать, что операторы и ⁺ действуют в разных пространствах.

Сумма эрмитовых и произведение эрмитовых коммутирующих операторов являются эрмитовыми операторами.

При применении оператора к вектору состояния может получиться тот же вектор, умноженный на некоторое число:

úYñ = úYñ F. (8.5)

Число F, удовлетворяющее равенству (8.5), в котором úYñ – отличный от нуля вектор состояния, называется собственным значением оператора , соответствующим собственному вектору úYñ, а этот вектор – собственным вектором, соответствующим данному собственному значению. Если в формуле вместо вектора стоит волновая функция Y, то ее называют собственной функцией оператора , соответствующей собственному значению F.

Бывает так, что одному и тому же собственному значению F соответствует несколько линейно не зависимых векторов или функций. Тогда это значение называют вырожденным, а число соответствующих состояний – кратностью вырождения. Линейная комбинация векторов (или функций), соответствующих собственному значению F, также является собственным вектором (функцией) оператора для того же собственного значения F.

В квантовой механике используются самосопряженные операторы благодаря их свойству, выражаемому следующей теоремой. Собственные значения самосопряженных операторов действительны, а их собственные векторы, соответствующие различным собственным значениям, ортогональны.

Ограничимся доказательством в отсутствии вырождения. Применим определение (8.5) к собственному значению F_i , а сопряженное с (8.5) выражение – к F_j: úiñ = úiñ F_i, ájç ⁺ = F_j*ájç. (8.6)

Умножив первое равенство слева на újñ, а второе – справа на áiç, получим после вычитания и учета самосопряженности оператора :

(F_i – F_j*) ájïiñ = ájï úiñ – ájï ⁺úiñ = 0. (8.7)

Если i = j, то из (8.7) следует F_i = F_j*, а для i ¹ j равно нулю скалярное произведение ájïiñ, то есть векторы újñ и úiñ ортогональны.

На основании этой теоремы можно утверждать, что множество собственных векторов самосопряженного оператора образует ортонормированный полный базис.

? Контрольные вопросы

1. Что такое оператор? Приведите примеры операторов.

2. Дайте определение линейного оператора.

3. Какие операторы называют нулевыми, единичными, равными?

4. Дайте определение суммы и произведения операторов.

5. Что такое коммутатор?

6. Расскажите о сопряженном операторе.

7. Дайте определение самосопряженного оператора.

8.

F

Какими свойствами обладают собственные значения и собственные векторы самосопряженного оператора?

Задания

Д. 8.1.Теорема о собственных значениях и собственных функциях самосопряженных операторов.

8.1. Докажите, что если [ ] = 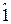, то [ ²] = 2 .

8.2. Докажите, что .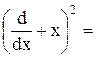

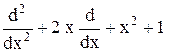8.3. Докажите соотношение (8.1).

8.4. Докажите соотношения (8.2).

8.5. Докажите, что сумма самосопряженных и произведение самосопряженных коммутирующих операторов являются самосопряженными операторами.

8.6. Докажите, что линейная комбинация векторов, соответствующих собственному значению F, также является собственным вектором оператора для того же собственного значения F.

Наблюдаемые

& Литература: [8], [3], [1], [7].

Наблюдаемыми в квантовой механике называют переменные величины, которые подлежат измерению. Предпринимались попытки построить теорию, в которой использовались не наблюдаемые переменные, «скрытые параметры».

Наблюдаемые в квантовой механике находятся посредством операторов. Постулируется, что каждой наблюдаемой F сопоставляется линейный самосопряженный оператор . Собственные значения этого оператора (действительные, так как оператор самосопряженный) равны тем значениям, которые рассматриваемая величина F может принимать на опыте. Собственные векторы описывают состояния, в которых наблюдаются соответствующие собственные значения.

Если объект находится в состоянии, описываемом собственным векторомúiñ оператора : ÷iñ = úiñ F_i, то при каждом измерении наблюдаемой величины F будет зарегистрировано значение F_i. Таково же будет и ее среднее значение. Система может оказаться в состоянии Y, которое не описывается собственным вектором оператора . Тогда в отдельных измерениях будут регистрироваться те или иные собственные значения F_i оператора , но с различной вероятностью.

Для нахождения этих вероятностей вектор úYñ можно разложить по собственным векторам úiñ оператора , поскольку они образуют полный базис: úYñ = 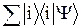. Коэффициенты этого разложения и дают вероятности i-го собственного значения: W_i = ÷áiïYñç² = áiïYñ* áiïYñ = áYïiñ áiïYñ. Среднее значение величины F находится по формуле

áFñ = 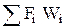= = 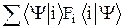= 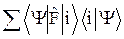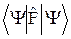. (9.1)

Совместность величин связана с коммутативностью сопоставляемых им операторов. Эта связь устанавливается теоремой о коммутирующих операторах. Необходимым и достаточным условием совместности наблюдаемых величин является коммутативность сопоставляемых им операторов.

Докажем необходимость этого условия. Пусть F и G – совместные величины. Это означат, что в состояниях ÷nñ, в которых F имеет определенные значения F_n, определенные значения G_n имеет и величина G. Тогда

÷nñ = ÷nñ F_n и (9.2)

÷nñ = ÷nñ G_n . (9.3)

Состояние ÷nñ в этом случае можно обозначить и так ÷F_n, G_nñ, подчеркнув тем самым, что вектор ÷nñ является общим для обоих операторов собственным вектором. Применив к обеим частям (9.2) оператор , а к (9.3) – оператор , получим после вычитания: ( – )÷nñ = [ ] ÷nñ = 0. Коммутативность операторов еще не доказана, поскольку нулевым называют оператор, который дает ноль при применении к произвольному вектору. Но общая для обоих операторов система собственных векторов ÷nñ образует полный базис, по которому можно разложить произвольный вектор ÷Yñ. Тогда получим: [ ] ÷Yñ = 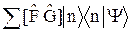= 0, так как каждое слагаемое равно нулю.

Докажем, что коммутативность операторов достаточна для совместностисопоставляемых им величин. Ограничимся случаем отсутствия вырождения. Для собственных векторов оператора запишем равенство (9.2). Применим к обеим частям равенства (9.2) оператор и учтем коммутативность операторов: ÷nñ = ( ÷nñ) = ( ÷nñ) F_n. Получается, что вектор ( ÷nñ) есть собственный для оператора , соответствующий собственному значению F_n. Но в (9.2) таковым является вектор ÷nñ. Одно состояние могут описывать разные векторы, если они отличаются постоянным множителем. Так что ÷nñ = ÷nñ G_n, то есть вектор÷nñ является собственным не только для оператора , но и для оператора . Величины, операторы которых имеют общие собственные векторы, совместны. Теорема доказана.

Теорему о коммутирующих операторах можно доказать и с учетом возможного вырождения.

? Контрольные вопросы

1. Что такое наблюдаемые величины?

2. Почему наблюдаемым величинам можно сопоставлять только самосопряженные операторы?

3. Какие значения величины F регистрируются в состоянии, описываемом собственным вектором оператора ?

4. Какие значения величины F регистрируются в произвольном состоянии?

5. Как найти среднее значение величины F в состоянии Y?

6. Чем замечательны операторы совместных величин?

F

Задания

Д. 9.1.Теорема о коммутирующих операторах.

9.1.Докажите, что exp(–x²/2) есть собственная функция оператора –d²/dx² + x², соответствующая собственному значению 1, а x exp(–x²/2) есть собственная функция того же оператора, соответствующая собственному значению 3.

9.2.Найдите собственные функции и собственные значения оператора –d²/dx², действующего на функции, определенные в области 0 £ x £ a и равные нулю на границах этой области. A sin 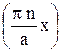, , 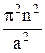n = 1, 2, 3,…