Оператор Гамильтона

Рассмотрев внимательно математическое содержание операций div, grad, rot (формулы 3.17, 3.18, 3.19), замечаем, что эти три соотношения могут быть представлены одним общим выражением вида:

(*)

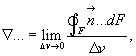где символ …, называемый оператором Гамильтона или вектором Набла, обозначает предел отношения, стоящий в правой части равенств 3.17, 3.18, 3.19.

Известна запись определения производной от функции

(**)

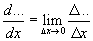Запись (*) и (**) имеют сходство и различие.

1. Сходство записей (*) и (**):

В записи (**) под знаком предела стоит разность значений (изменения) функции на границах интервала Δx, отнесенная к величине самого интервала.

В записи (*) также под знаком предела стоит отношение изменения (разности) значений некоторой величины (представляемое интегралом по поверхности) на границах интервала к самому интервалу ΔV.

Однако в выражении (**) рассматривается линейный интервал, в в выражении (*) трехмерный.

Поэтому знак можно трактовать, подобно символу 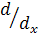, как оператор дифференцирования, но не по одной координате, а по всем трем координатам сразу, т.е. по объему.

2. Различие записей (*) и (**)

Известно, что оператор 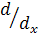, примененный к скалярной функции, всегда дает скалярную величину, а к векторной – векторную. Но мы ранее установили, что дивергенция вектора – скаляр, градиент скаляра – вектор, ротор вектора – вектор.

Т.е., казалось бы, применение оператора дифференцирования к векторным и скалярным функциям не приводит к однозначности результатов. Однако будем считать, что знак 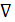имеет двойственную природу, являясь одновременно и оператором дифференцирования, и особым символическим вектором, т.е. вектором, не имеющим не определенной длины, ни направления.

Замечание:

Исходя из двойственности (двойственной природы) символа , строится изящное исчисление, широко применяемое в векторном анализе.

т.о.

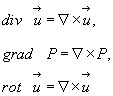(3.23)

∙ - есть скалярное произведение вектора набла на вектор скорости (и в то же время определенным образом выполненное дифференцирование), поэтому ясно, что дивергенция вектора есть скорость.

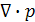- есть вектор (умножение вектора на скаляр), но в то же время осуществляется дифференцирование скалярной функции по объему.

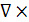
- есть векторное произведение вектора набла на вектор скорости, что дает производный вектор получившийся в результате определенным образом проведенного дифференцирования векторной функции по объему.

Замечание:

В векторном анализе в основном действуют все те правила, которые справедливы для дифференциального исчисления обычных скалярных функций, однако имеется и некоторое отличие.