Векторные и матричные операторы
Для работы с векторами и матрицами Mathcad имеет ряд операторов и функций. Рассмотрим вначале операторы, введя следующие обозначения:
для векторов V, для матрицы Ми для скалярных величин Z.
Оператор Назначение
V1+V2 Сложение векторов V1 и V2.
V1-V2 Вычитание векторов V1 и V2
-V Смена знака у элементов вектора V.
-M Смена знака у элементов матрицы M.
V-Z Вычитание из вектора V скаляра Z.
Z×V V×Z Умножение вектора V на скаляр Z.
Z×M M×Z Умножение матрицы M на скаляр Z
V1×V2 Умножение векторов V1 и V2.
M×V Умножение матрицы M на вектор V.
M1×M2 Умножение матриц M1 и M2.
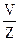 Деление вектора V на скаляр Z
Деление вектора V на скаляр Z
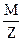 Деление матрицы на скаляр Z
Деление матрицы на скаляр Z
M-1 Обращение матрицы M.
Mn Возведение матрицы M в степень n
|V| Модуль вектора V
|M| Определитель матрицы M
VT Транспонирование вектора V
MT Транспонирование матрицы M
V1xV2 Кросс умножение векторов V1 и V2
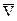 Комплексно-сопряженный вектор от V
Комплексно-сопряженный вектор от V
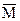 Комплексно-сопряженная матрица от М
Комплексно-сопряженная матрица от М
SV Сумма элементов вектора V
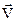 Векторизация вектора V
Векторизация вектора V
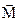 Векторизация матрицы M
Векторизация матрицы M
M<n> Выделение столбца (n) из матрицы М
Vn Выделение элемента (n) из вектора V
Mm,n Выделение элемента (m,n) из матрицы М
Операция векторизации понимается, как одновременное исполнение математических операций в их скалярном значении над всеми элементами вектора или матрицы, помеченных символом векторизации.
Матричные операторы находятся на палитре «Матрицы»:
 Шаблон матрицы/вектора, Индексированная переменная, Обратная матрица, Определитель,
Шаблон матрицы/вектора, Индексированная переменная, Обратная матрица, Определитель,
Векторизация, Выделение столбца матрицы, Транспонирование, Границы одномерного массива,
Внутреннее произведение векторов, Кросс произведение векторов, Сумма вектора, Картинка.
7.2. Векторные и матричные функции
Для их вставки используется команда Insert /Function…/Vector and Matrix или кнопка f(x) панели инструментов.
Векторные функции
length(V) - длина вектора V.
max(V) - максимальный элемент вектора V.
min(V) - минимальный элемент вектора V.
mean(V) - среднее арифметическое значение элементов V.
Re(V) - вещественный вектор от V. //Создает вектор из вещественных частей
элементов комплексного вектора V
Im(V) - мнимый вектор от V. // Создает вектор из мнимых частей
элементов комплексного вектора V
Матричные функции
cols(M) - число столбцов матрицы M.
rows(M) - число строк матрицы M.
tr(М) - след матрицы M. Возвращает сумму диагональных элементов матрицы М.
mean(M) - среднее значение массива M. Среднее арифметическое.
augment(M1,M2) - объединить матрицы М1,М2. Объединяет в одну матрицы M1 и M2
с одинаковым числом строк. М2 справа от М1.
stack(M1,M2) - объединить матрицы М1,М2. Объединяет в одну матрицы M1 и M2
с одинаковым числом столбцов. М2 под М.
identity(n) - единичная матрица размером n*n. Создает квадратную матрицу
размером n*n и присваивает ее элементам значения 1.
submatrix(М,ir,jr,ic,jc) - субматрица. Возвращает субматрицу из элементов в строках
от ir до jr и в столбцах от ic до jc матрицы М.
diag(V) - диагональная матрица. Создает диагональную матрицу, в главной
диагонали которой размещается вектор V.
matrix(m,n,f) - матрица с заданным элементом. Создает матрицу, элементом которой
является значение функции f(i,j). I=0…m, j=0…n.
Re(M)- вещественная матрица от M. Создает матрицу из вещественных частей
элементов комплексной матрицы M.
Im(М)- мнимая матрица от М. Создает матрицу из мнимых частей элементов
комплексной матрицы M.
7.3. Функции сортировки для векторов и матриц
sort(V) - сортировка элементов вектора V. Сортирует по возрастанию элементы в V
revers(V) - переставляет элементы вектора V в обратном порядке исходного вектора
csort(M,n) - сортировка матрицы по столбцу. Переставляет строки матрицы М таким
образом, чтобы отсортированным оказался столбец n
rsort(M,k) - сортировка матрицы по столбцу. Переставляет столбцы матрицы М таким
образом, чтобы отсортированным оказалась строка k.
Рассмотрим примеры векторных и матричных операторов и функций.
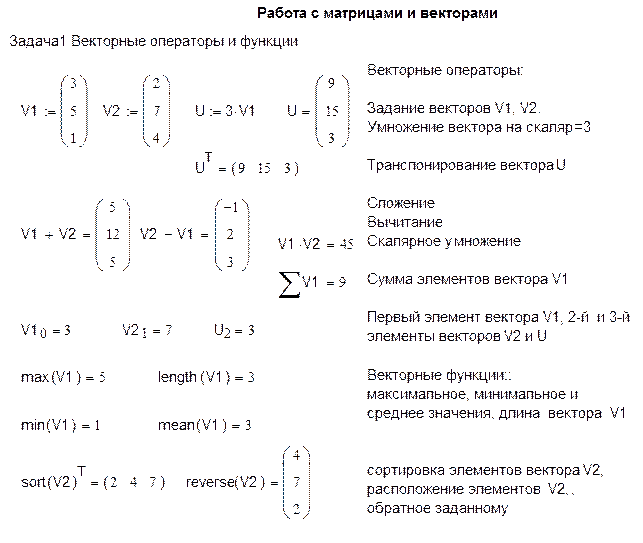

Дата добавления: 2019-12-09; просмотров: 1001;











