Ответ содержится в последней строке таблицы.
Задача 5. Решить систему линейных уравнений методом Гаусса-Зейделя с точностью 0,05:
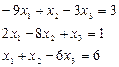
Аналогично проверяем условие диагонального преобладания.
Разрешим систему уравнений относительно 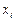
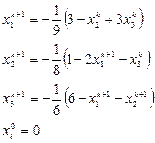
Результаты удобно оформить в таблицу
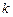
| 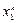
| 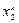
| 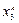
| 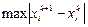
|
| -0.33333 | -0.20833 | -1.09028 | 1.090278 | |
| 0.006944 | -0.25955 | -1.0421 | 0.340278 | |
| -0.01481 | -0.25896 | -1.04563 | 0.02175 |
Ответ содержится в последней строке таблицы.
Задача 6. Для таблично заданной функции:
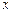
| -2 | 1,5 | ||
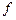
| 0,1 | -0,2 | 0,5 | 1,2 |
вычислить значение функции в точке z=1,2, используя формулы линейной интерполяции.
Определяем интервал, которому принадлежит 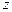 :
:  .
.
Расчетные формулы:
 .
.
Тогда
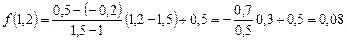 .
.
Ответ: 0,08.
Задача 7. Для таблично заданной функции:
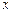
| -2 | 1,5 | ||
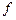
| 0,1 | -0,2 | 0,5 | 1,2 |
выписать базисные полиномы и вычислить значение полинома Лагранжа в точке z=1,2; при n=3.
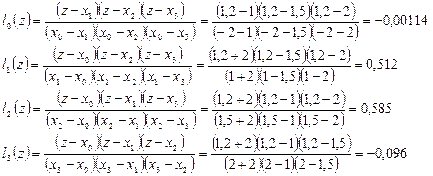
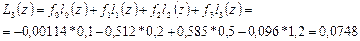
Ответ: 0,0748.
Примеры решения задач на интегрирование можно найти выше.
Рекомендации. В билетах задание может быть в виде:
Вычислить интеграл методом трапеций функции, заданной таблично:
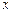
| -1 | -0,5 | ||
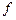
| 4,5 |
В данном задании переменная 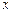 меняется с постоянным шагом 0,5. При использовании формулы трапеций решение ищется в виде:
меняется с постоянным шагом 0,5. При использовании формулы трапеций решение ищется в виде:
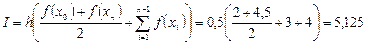 .
.
В случае же, если шаг не постоянный, например:
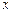
| -1 | -0,6 | 0,8 | |
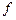
| 4,5 |
необходимо пользоваться общей формулой трапеций:
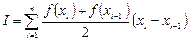
Т.е. в данном случае решение ищется как
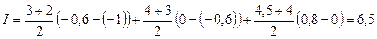
Аналогично для формул левых и правых прямоугольников:
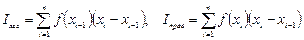 .
.
Дата добавления: 2021-09-07; просмотров: 513;











