Приближенные методы решения задачи Коши для ОДУ первого порядка

Требуется найти решение y(x) ОДУ первого порядка

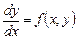(5.2)

на отрезке 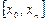при условии

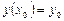. (5.3)

Приближенное решение будем искать в узлах расчетной сетки 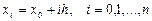с шагом 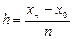. Необходимо найти приближенные значения в узлах сетки y_i=y(x_i). Результаты расчетов занесем в таблицу

			…
			…

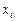
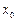
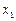
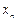
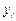
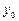
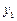
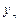
Интегрируя уравнение на отрезке 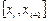, получим

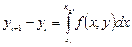. (5.4)

Для того, чтобы найти все значения 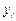, нужно каким-то образом вычислить интеграл, стоящий в правой части (5.4). Применяя различные квадратурные формулы, будем получать методы решения задачи (5.2), (5.3) разного порядка точности.

Метод Эйлера

Если для вычисления интеграла в (5.4) воспользоваться простейшей формулой левых прямоугольников первого порядка

,

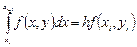то получим явную формулу Эйлера:

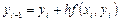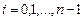, . (5.5)

Явный метод Эйлера имеет первый порядок аппроксимации. Реализация метода. Поскольку 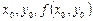известны, применяя (5.5) последовательно, определим все y_i: , , ….

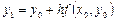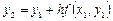Геометрическая интерпретация метода Эйлера (рис. 5.1.):

Пользуясь тем, что в точке 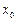известно решение 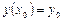и значение его производной 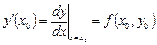, можно записать уравнение касательной к графику искомой функции 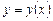в точке 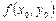: 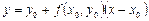. При достаточно малом шаге 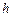ордината 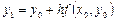этой касательной, полученная подстановкой в правую часть значения 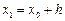, должна мало отличаться от ординаты 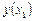решения 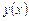задачи Коши. Следовательно, точка 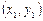пересечения касательной с прямой 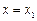может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую 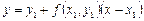, которая приближенно отражает поведение касательной к 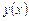в точке 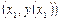. Подставляя сюда 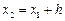(т.е. пересечение с прямой 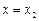), получим приближенное значение 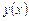в точке 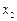: 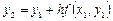и т.д. В итоге для 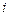-ой точки получим формулу Эйлера.

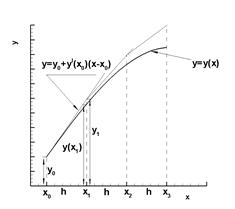
Рис. 5.1. Геометрическая интерпретация метода Эйлера

Если в (5.4) использовать формулу правых прямоугольников: 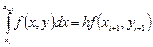, то получим неявныйметод Эйлера

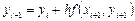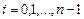, . (5.6)

Этот метод называют неявным, поскольку для вычисления неизвестного значения 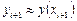по известному значению 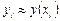требуется решать уравнение, в общем случае нелинейное. Неявный метод Эйлера также имеет первый порядок аппроксимации.