Численные методы решения систем ОДУ первого порядка
Рассмотренные выше методы решения задачи Коши для одного уравнения могут быть использованы также для решения систем дифференциальных уравнений первого порядка и уравнений высших порядков.
Пусть задана задача коши для системы двух уравнений первого порядка:
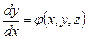
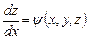
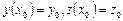
Обобщим формулы явного метода Эйлера (5.5):
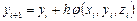
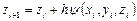 ,
,
модифицированного метода Эйлера (5.7):
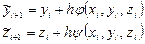
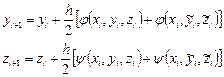 ,
,
схемы Рунге-Кутта четвертого порядка точности (5.10):
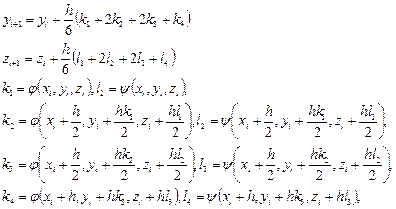
Вычисления приближенного решения проводятся путем последовательного применения этих формул.
Рассмотрим задачу Коши для уравнения второго порядка
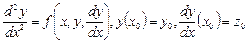
Введем вторую неизвестную функцию 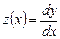 . Тогда исходная задача Коши для уравнения сводится к следующей задаче для системы двух ОДУ первого порядка:
. Тогда исходная задача Коши для уравнения сводится к следующей задаче для системы двух ОДУ первого порядка:
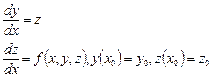 ,
,
которая решается с помощью методов, описанных выше.
ПРИМЕР 5.2. Найти решение задачи Коши:
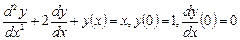 на отрезке
на отрезке 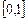 .
.
Точное решение: 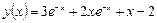 .
.
Проверим, что точное решение удовлетворяет данному дифференциальному уравнению. Действительно:
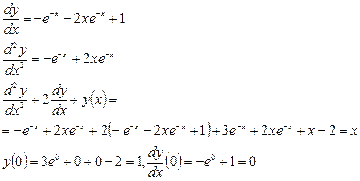
Решим задачу явным методом Эйлера (5.5), модифицированным методом Эйлера (5.7) и методом Рунге-Кутты (5.10) на сетке с шагом 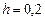 .
.
Введем функцию 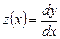 и получим следующую задачу Коши для системы двух ОДУ первого порядка:
и получим следующую задачу Коши для системы двух ОДУ первого порядка:
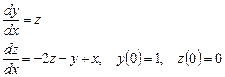 .
.
Используем формулы явного метода Эйлера:
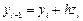
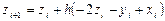
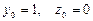 ,
,
модифицированного метода Эйлера:
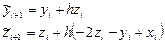
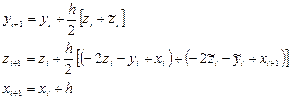 .
.
четырехэтапного метода Рунге – Кутты:
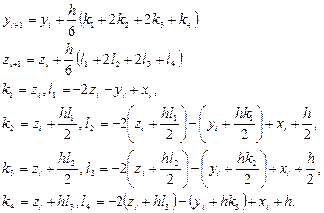
Решение оформим в виде таблиц.
Схема Эйлера:
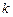
| 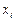
| 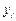
| 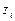
| Точное решение | Погрешность |
| 0.2 | -0.2 | 0.983685 | 0.016315 | ||
| 0.4 | 0.96 | -0.28 | 0.947216 | 0.012784 | |
| 0.6 | 0.904 | -0.28 | 0.905009 | 0.001009 | |
| 0.8 | 0.848 | -0.2288 | 0.866913 | 0.018913 | |
| 0.80224 | -0.14688 | 0.839397 | 0.037157 |
Модифицированный метод Эйлера:
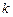
| 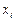
| 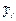
| 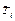
| 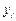
| 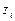
| Точ.реш | Погреш. |
| 0.2 | -0.2 | -0.18 | 0.983685 | 0.016315 | |||
| 0.4 | 0.964 | -0.268 | 0.962 | -0.244 | 0.947216 | 0.014784 | |
| 0.6 | 0.9132 | -0.2588 | 0.9108 | -0.2342 | 0.905009 | 0.005791 | |
| 0.8 | 0.86396 | -0.20268 | 0.8615 | -0.178 | 0.866913 | 0.005413 | |
| 0.8259 | -0.1191 | 0.823432 | -0.09441 | 0.839397 | 0.015965 |
Схема Рунге-Кутта:
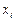
| 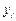
| 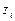
| 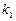
| 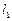
| 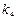
| 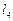
| Погреш. |
| 0.2 | 0.9837 | -0.146 | -1 | -0.15 | -0.486 | 1.79E-05 | |
| 0.4 | 0.9472 | -0.207 | -0.146 | -0.491 | -0.209 | -0.13 | 2.76E-05 |
| 0.6 | 0.905 | -0.207 | -0.207 | -0.134 | -0.209 | 0.113 | 3.18E-05 |
| 0.8 | 0.8669 | -0.168 | -0.207 | 0.1097 | -0.17 | 0.272 | 3.25E-05 |
| 0.8394 | -0.104 | -0.168 | 0.2695 | -0.105 | 0.37 | 3.09E-05 |
Как можно видеть, максимальная погрешность, определяемая как разность между точным и рассчитанным значением функции 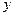 , в методе Рунге-Кутта не превышает
, в методе Рунге-Кутта не превышает 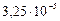 .
.
Дата добавления: 2021-09-07; просмотров: 576;











