ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ И РЕКОМЕНДАЦИИ К ЭКЗАМЕНУ

Задача 1. Получить решение уравнения 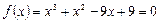методом деления отрезка пополам с точностью 0,05. Интервал изоляции .

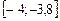Проверим, что данных отрезок является интервалом изоляции корня. Найдем значение функции на концах этого интервала: 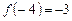, 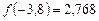. Т.е. на интервале содержится корень уравнения. Проверим, что он единственный.

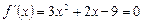
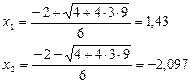
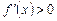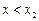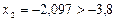Следовательно, на всем интервале , а , т.е. функция 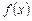монотонно возрастающая на 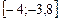, следовательно, данный интервал содержит один корень уравнения и является интервалом изоляции.

Расчеты проведем в Excel по методу деления отрезка пополам, результаты оформим в виде таблицы.

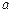
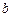
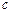
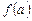
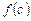
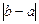
	-4	-3.8	-3.9	-3	-0.009	0.2
	-3.9	-3.8	-3.85	-0.009	1.405875	0.1
	-3.9	-3.85	-3.875	-0.009	0.705078	0.05
	-3.9	-3.875	-3.8875	-0.009	0.349705	0.025

Расчетные формулы:

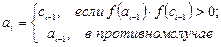
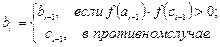
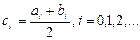
Ответ: x=-3.8875

Задача 2. Получить решение уравнения 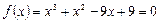методом простой итерации с точностью 0.001. Интервал изоляции .

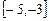Аналогично доказываем, что интервал является интервалом изоляции.

,

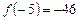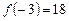
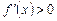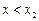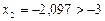на всем интервале , а , т.е. функция 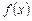монотонно возрастающая на 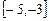, следовательно, данный интервал является интервалом изоляции.

Расчетные формулы:

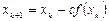
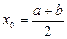
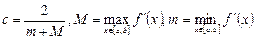
Найдем значения констант. Для этого вычислим значения первой и второй производных:

.

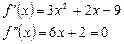Экстремум производной функции находится в точке

.

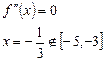Находим значения производной на концах отрезка

.

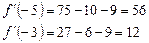Таким образом, .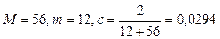

, .

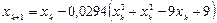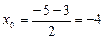Вычисления оформляем в таблице

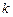
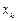
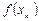
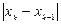
	-4	-3
	-3.9118	-0.35069	0.0882
	-3.90149	-0.05198	0.01031
	-3.89996	-0.0079	0.001528
	-3.89973	-0.0012	0.000232

Ответ: x= -3,8997

Задача 3. Получить решение уравнения 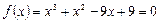методом Ньютона с точностью 0,001. Интервал изоляции .

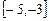Проверка значений интервала изоляции была сделана в примере выше. Расчетные формулы метода Ньютона:

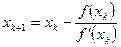или в нашем случае

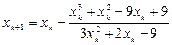
Выбираем нулевое приближение. 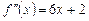, , 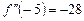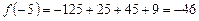. Знак функции и знак второй производной совпадают на правом конце отрезка, поэтому выбираем его в качестве начального приближения .

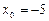Результаты представлены в таблице

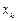
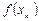
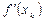
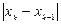
	-5	-46
	-4.17857	-8.89217	35.02423	0.821429
	-3.92469	-0.72721	29.36009	0.253886
	-3.89992	-0.00659	28.82821	0.024769
	-3.89969	-5.6E-07	28.82332	0.000229

Ответ: x=-3,89969

Задача 4. Решить систему линейных уравнений методом простой итерации с точностью 0,05:

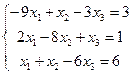
Проверим условие диагонального преобладания:

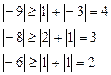
Условия диагонального преобладания выполняются.

Разрешим систему уравнений относительно

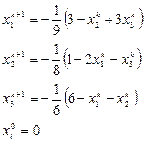
Результаты можно представить в виде таблицы

				–
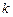
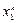
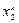
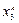
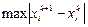
	-0.33333	-0.125	-1
	-0.01389	-0.33333	-1.07639	0.319444
	-0.01157	-0.26302	-1.05787	0.070313
	-0.00993	-0.26013	-1.04577	0.012105