Модифицированный метод Эйлера

В данном методе вычисление 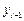состоит из двух этапов:

,

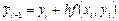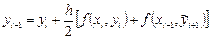. (5.7)

Данная схема называется также методом предиктор-корректор. Это английское название, означающее «предсказать-исправить». Действительно, на первом этапе приближенное значение предсказывается с первым порядком точности, а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности.

Методы Рунге-Кутты

Идея построения явных методов Рунге-Кутты 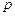-го порядка заключается в получении приближений к значениям 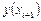по формуле вида 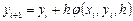, где

,

,

,

…

.

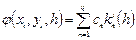
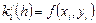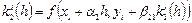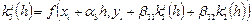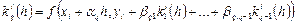Здесь 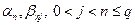– некоторые фиксированные числа (параметры), которые подбирают таким образом, чтобы получить нужный порядок аппроксимации p. Как правило, для каждого p существует не одна схема Рунге-Кутты порядка p, а целое параметрическое семейство. Так, схемы Рунге-Кутта второго порядка точностиобразуют однопараметрическое семейство

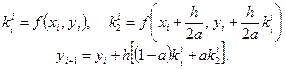(5.8)

Выделим из семейства методов (5.8) два наиболее простых и часто используемых частных случая. При 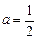получаем формулы

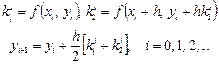, (5.9)

которые совпадают с формулами модифицированного метода Эйлера (5.7). При a=1 выводим новый простой метод

,

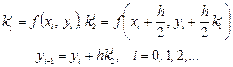который называется методом средней точки.

Схема Рунге-Кутта четвертого порядка точности.При p=4 можно получить один из вариантов метода:

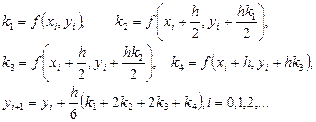(5.10)

ПРИМЕР 5.1. Решить задачу Коши:

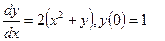на отрезке 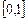с шагом 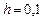с помощью явного метода Эйлера (5.5), модифицированного метода Эйлера (5.7) и четырехэтапного метода Рунге-Кутта (5.10). Точное решение: .

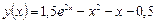Построим разностную сетку .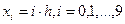

Расчетные формулы по явному методу Эйлера для данного примера: , .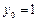

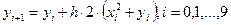Расчетные формулы модифицированного метода Эйлера: , , ,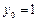

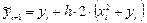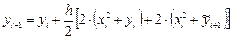Расчетные формулы метода Рунге-Кутта:

,

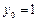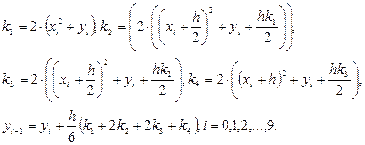
Результаты вычислений в Excel приведены ниже

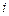
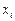
		Эйлер		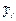Модиф. Эйлер	Рунге-Кутта	Точное
	0.1	1.2	1.2	1.22	1.218393	1.222104
	0.2	1.442	1.462	1.488593	1.488609	1.497737
	0.3	1.7384	1.788993	1.824368	1.826287	1.843178
	0.4	2.10408	2.200166	2.24674	2.250465	2.278311
	0.5	2.556896	2.718774	2.779016	2.784329	2.827423
	0.6	3.118275	3.372771	3.449508	3.456112	3.520175
	0.7	3.81393	4.196062	4.292669	4.300192	4.3928
	0.8	4.674716	5.229881	5.350447	5.358432	5.489549
	0.9	5.73766	6.524423	6.673919	6.68181	6.864471
		7.047191	8.140804	8.325282	8.332399	8.583584

Видно, что в сравнении с точным решением, самым точным является метод Рунге – Кутта.