ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Постановка задачи

Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать в виде:

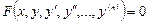, (5.1)

где 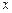– независимая переменная, 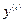‑ 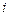-ая производная от искомой функции, 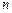– порядок уравнения. Общее решение ОДУ 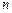-го порядка содержит 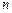произвольных постоянных 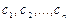, т.е. общее решение имеет вид .

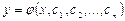Для выделения единственного решения необходимо задать 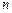дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.

Ясно, что при 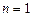можно говорить только о задачи Коши.

Примеры постановки задачи Коши:

;

.

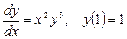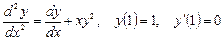Примеры краевых задач:

.

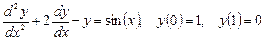
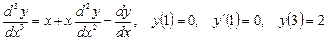Решить такие задачи аналитически удается лишь для некоторых специальных типов уравнений, поэтому применение приближенных методов решения является необходимостью.