Подбор эмпирических формул

При интерполировании функций мы использовали условие равенства значений интерполяционного полинома и данной функции в узлах интерполяции. Если же исходные данные получены в результате опытных измерений, полученных с некоторой погрешностью, точного выполнения условий интерполяции не требуется. В этих случаях интерполирующая функция F(x) должна удовлетворять условиям 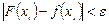, i=1, 2, …, N. Это условие означает, что интерполирующая функция 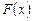проходит не точно через заданные точки, а в некоторой их окрестности, как, например, показано на рис. 3.3.

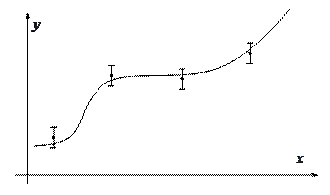
Рис. 3.3. Приближенная интерполяция

Тогда говорят о подборе эмпирических формул,описывающих заданные точки. Построение эмпирической формулы состоит из двух этапов: подбора вида этой формулы 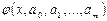, содержащей неизвестные параметры 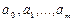, и определение наилучших в некотором смысле этих параметров. Вид формулы иногда известен из физических соображений (например, связь между напряжением и деформацией для упругой среды), или выбирается из геометрических соображений. Для этого экспериментальные точки наносятся на график и путем сравнения поведения точек с графиками известных функций подбирается общий вид зависимости. Успех в значительной степени определяется опытом и интуицией исследователя.

Для практики важен случай аппроксимации функции многочленами, т.е. .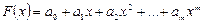

После того, как выбран вид эмпирической зависимости, степень близости к эмпирическим данным определяется, используя минимум суммы квадратов отклонений вычисленных и экспериментальных данных.