Метод наименьших квадратов

Пусть для исходных данных выбран вид эмпирической зависимости: с неизвестными коэффициентами 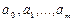. Запишем сумму квадратов отклонений между вычисленными по эмпирической формуле и заданными опытными данными:

.

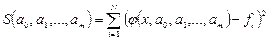Параметры 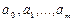будем находить из условия минимума функции 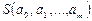. В этом состоит метод наименьших квадратов (МНК).

Известно, что в точке минимума все частные производные от 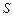по параметрам 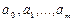равны нулю:

(3.2)

Рассмотрим применение МНК для частного случая, широко используемого на практике. В качестве эмпирической функции рассмотрим полином

.

Формула (3.2) для определения суммы квадратов отклонений примет вид:

(3.3)

Вычислим производные:

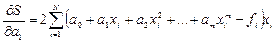
Приравнивая эти выражения нулю, и собирая коэффициенты при неизвестных 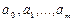, получим следующую систему линейных уравнений:

.

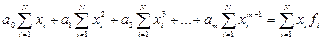Данная система уравнений называется нормальной. В результате решения этой системы линейных уравнений одним из известных способов, находятся коэффициенты .

В случае полинома первого порядка , т.е. , система нормальных уравнений примет вид:

.

При имеем:

.

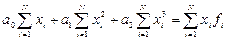Как правило, выбирают несколько эмпирических зависимостей. По МНК находят коэффициенты этих зависимостей и среди них находят наилучшую по минимальной сумме отклонений.

ПРИМЕР 3.4.Заданы координаты 6 точек:

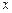
	-5	-3,5	-2	1,5	3,25
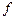
	0,5	1,2	1,4	1,6	1,7	1,5

Требуется по методу МНК найти эмпирические зависимости: линейную , квадратичную 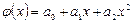, гиперболическую , и выбрать среди них наилучшую по наименьшей сумме квадратов отклонений.

Система нормальных уравнений для линейной зависимости:

,

.

Учитывая, что 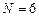, и, используя Excel, находим:

,

,

,

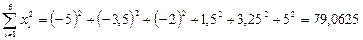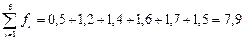В итоге получим СЛАУ

.

Решая систему линейных уравнений, получим , . Следовательно, линейная зависимость имеет вид: .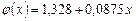

Вычислим сумму квадратов отклонений: .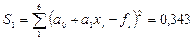

Рассмотрим квадратичную зависимость. Система нормальных уравнений имеет вид

.

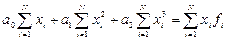Часть из сумм уже найдена при подборе линейной зависимости. Используя Excel, найдем оставшиеся суммы: , , .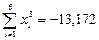

Решая нормальную систему уравнений:

,

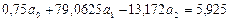
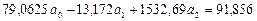получим: , , .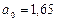

Следовательно, квадратичная зависимость имеет вид: 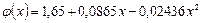. Вычислим сумму квадратов отклонений: .

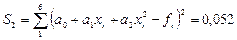Выпишем систему нормальных уравнений для гиперболической зависимости. Согласно МНК, находим сумму квадратов отклонений:

.

Составляем систему нормальных уравнений:

Или

Учитывая, что , , , 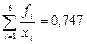получим 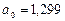, . Зависимость имеет вид .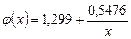

Сумма квадратов отклонений: .

Итак, минимальным отклонением из трех рассмотренных зависимостей обладает квадратичная, т.е., она является лучшей из данных трех для аппроксимации исходных данных.

Графически результаты расчетов представлены на рис. 3.4. Маркерами отмечены исходные данные. Видно, что квадратичная зависимость действительно проходит ближе всего к заданным значениям функции.