Естественный способ задания движения
При естественном способе задания движения задаются траектория и закон движения точки по траектории. Траектория принимается в качестве криволинейной оси. На траектории выбирается точка О, принимаемая за начало отсчета расстояний, и положительное направление отсчета (например, вправо, рис. 2.3). Закон движения точки по траектории задается зависимостью от времени расстояния s, отсчитываемого от точки О до точки М, то есть 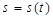 . Эта функция должна быть непрерывной и дважды дифференцируемой. Расстояние s , берется по траектории.
. Эта функция должна быть непрерывной и дважды дифференцируемой. Расстояние s , берется по траектории.
 |
Рисунок 2.3
Для определения скорости и ускорения необходимо ввести некоторые геометрические понятия. На рис. 4 показаны две близкие точки М и М1 пространственной кривой и проведены касательные к кривой в этих точках М и М1. В точке М проведена прямая  параллельная М1.
параллельная М1.
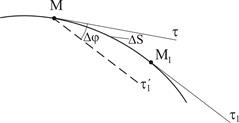
Рисунок 2.4
Угол Δφ между смежными касательными называется углом смежности. Кривизной кривой в точке М называется предел 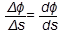 .
.
Радиусом кривизны кривой в точке М называют величину, обратную кривизне кривой 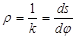 .
.
Введем естественные оси кривой (рис.2.5). Первой естественной осью является касательная Мτ. Ее положительное направление совпадает с направлением единичного вектора касательной 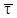 , направленного в сторону возрастающих расстояний. Перпендикулярно касательной располагается нормальная плоскость. Нормаль Mn, расположенная в соприкасающейся плоскости, называется главной нормалью. По главной нормали внутрь вогнутости кривой направляется единичный вектор
, направленного в сторону возрастающих расстояний. Перпендикулярно касательной располагается нормальная плоскость. Нормаль Mn, расположенная в соприкасающейся плоскости, называется главной нормалью. По главной нормали внутрь вогнутости кривой направляется единичный вектор 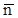 . Он определяет положительное направление второй естественной оси. Нормаль Mb, перпендикулярная главной нормали, называется бинормалью. По бинормали направлен единичный вектор
. Он определяет положительное направление второй естественной оси. Нормаль Mb, перпендикулярная главной нормали, называется бинормалью. По бинормали направлен единичный вектор 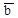 таким образом, чтобы три вектора
таким образом, чтобы три вектора 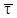 ,
, 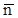 ,
, 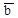 образовывали правую систему осей координат. Оси Mτ, Mn, Mb называются естественными осями кривой.
образовывали правую систему осей координат. Оси Mτ, Mn, Mb называются естественными осями кривой.
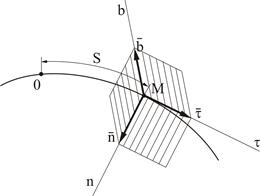 |
Рисунок 2.5
При движении точки по траектории ее радиус-вектор изменяется с течением времени, и изменяется в зависимости от расстояния S (рис.2.6).
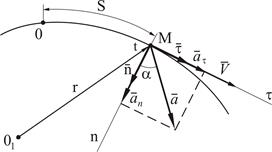
Рисунок 2.6
Используя определение скорости, получим 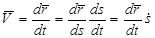 или
или
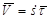 , (2.12)
, (2.12)
где 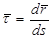 - единичный вектор касательной.
- единичный вектор касательной.
Учитывая, что для скорости точки имеем 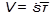 , в соответствии с определением ускорения получаем
, в соответствии с определением ускорения получаем 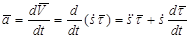
Учитывая математическое выражение 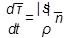 , получим
, получим
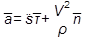 , (2.13)
, (2.13)
где 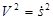 ,
,
ρ - радиус кривизны
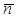 - единичный вектор главной нормали.
- единичный вектор главной нормали.
Часть ускорения 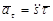 называется касательной составляющей ускорения. Другая часть ускорения
называется касательной составляющей ускорения. Другая часть ускорения 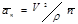 называется нормальной составляющей ускорения.
называется нормальной составляющей ускорения.
Таким образом ускорение точки при естественном способе задания —
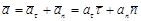
где 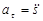 - касательное ускорение,
- касательное ускорение,
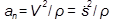 - нормальное ускорение
- нормальное ускорение
Учитывая ортогональность 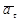 и
и 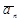 получим следующее выражения для модуля полного ускорения и угла между полным ускорением и нормалью
получим следующее выражения для модуля полного ускорения и угла между полным ускорением и нормалью
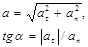 .
.
Нормальная составляющая ускорения 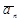 всегда направлена внутрь вогнутости траектории. Касательная составляющая
всегда направлена внутрь вогнутости траектории. Касательная составляющая 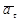 при
при 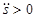 направлена в положительную сторону касательной, а при
направлена в положительную сторону касательной, а при 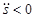 - в отрицательную, то есть противоположно
- в отрицательную, то есть противоположно 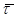 .
.
Пример определения скорости и ускорения точки по заданным уравнениям ее движения. По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t=t1c найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в соответствующей точке.

Решение. Уравнения движения являются параметрическими уравнениями траектории точки М. Чтобы получить уравнение траектории в обычной координатной форме, исключим время t из уравнений движения. Из этих уравнений получим
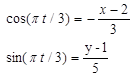 (2.16)
(2.16)
Подставляя в тригонометрическое тождество 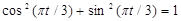 выражения (2.16) , получим
выражения (2.16) , получим 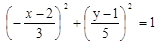 или
или
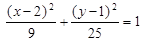 (2.17)
(2.17)
Это выражение есть уравнение смещенного эллипса с полуосями a=3 сми b=5 см. Центр эллипса находится в точки с координатами x=2 см и y=1 см. (рис. 2.7). В начальный момент ( 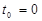 ) времени по уравнениям (2.14) и (2.15) получим координаты начальной точки М0
) времени по уравнениям (2.14) и (2.15) получим координаты начальной точки М0
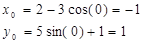
Для заданного момента времени t=t1=1 c получим
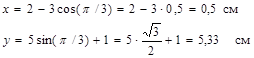
Для определения скорости точки находим проекции скорости на оси координат:
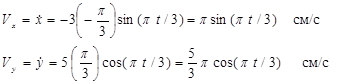
Для заданного момента времени t=t1=1 c получим
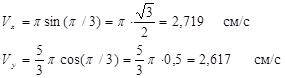
Модуль скорости точки
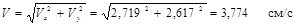 (2.18)
(2.18)
Аналогично проекции ускорения точки
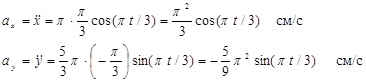
Для заданного момента времени t=t1=1 c получим
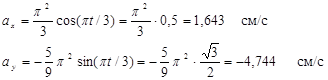
Модуль ускорения точки

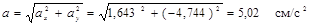
Координаты точки, а также ее скорость, ускорение и их проекции на координатные оси для заданного момента времени t=1 с приведены в таблице 1.
Таблица 1
| Коорди наты, см | Скорость, см/с | Ускорение, см/с2 | Радиус кривизны, см | |||||||
| x | y | Vx | Vy | V | ax | ay | a | a | an | ρ |
| 0,5 | 5,33 | 2,719 | 2,617 | 3,774 | 1,643 | 4,744 | 5,02 | -2,106 | 4,557 | 3,126 |
Касательное ускорение находим путем дифференцирования модуля скорости (2.18):
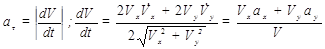
При t=1с 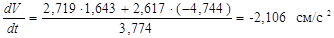
Следовательно, модуль касательного ускорения 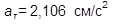 .
.
Знак «-» при dV/dt показывает, что движение точки замедленное. Нормальное ускорение точки в данный момент времени
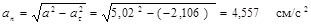
Радиус кривизны траектории в той точке, где при t=1 находится точка М, 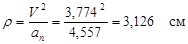 .
.
Пользуясь уравнением (2.17), строим траекторию (рис. 2.7) и показываем на ней положение точки М в заданный момент времени. Вектор 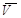 строим по составляющим
строим по составляющим 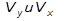 , причем этот вектор должен быть направлен по касательной к траектории точки. Вектор
, причем этот вектор должен быть направлен по касательной к траектории точки. Вектор 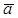 cтроим как по составляющим
cтроим как по составляющим 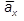 ,
, 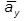 так и по составляющим
так и по составляющим 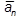
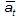 , чем контролируется правильность вычислений.
, чем контролируется правильность вычислений.
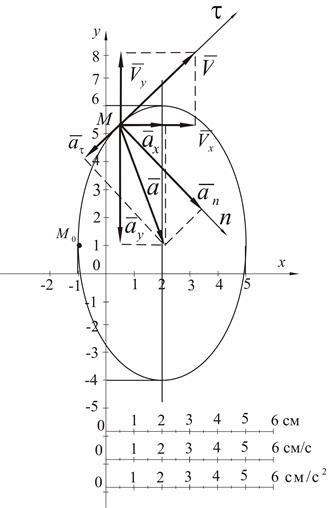
Рисунок 2.7
Дата добавления: 2017-06-13; просмотров: 2793;











