Координатный способ задания движения

В качестве системы отсчета рассмотрим декартовы оси координат, относительно которых рассматривается движение точки (рис. 2.2). Движение точки в декартовых координатах считается заданным, если известны координаты точки как непрерывные, дважды дифференцируемые функции времени, то есть заданы уравнения движения точки в декартовых координатах

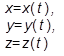(2.4)

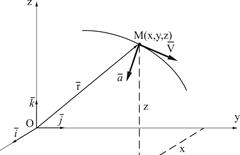
Рисунок 2.2

Уравнение траектории в координатной форме получают исключением из уравнений (2.4) времени t. Разложим радиус-вектор на составляющие параллельные осям координат

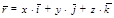(2.5)

где x, y, z – координаты точки М; 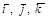- единичные векторы осей координат.

Учитывая выражение (2.5), согласно определению скорости имеем

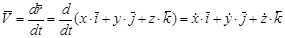(2.6)

В соответствии с выражением (6) получаем следующие формулы для проекций скорости на декартовы оси координат

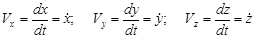(2.7)

По проекциям определяем числовое значение (модуль) скорости и направляющие косинусы углов вектора скорости с осями координат

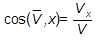
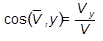
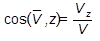(2.8)

Учитывая выражение (2.6), согласно определению ускорения имеем

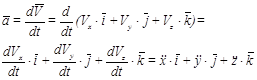(2.9)

В соответствии с выражением (2.9) получаем следующие формулы для проекций ускорения на декартовые оси координат

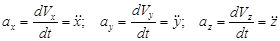(2.10)

По проекциям определяем числовое значение (модуль) ускорения и косинусы углов вектора ускорения с осями координат

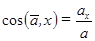
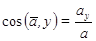
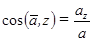(2.11)