Приведение произвольной системы сил к заданному центру.

Точку, к которой приводят систему сил, называют центром приведения данной системы сил. Пусть на твердое тело (рис.1.15) действует произвольная система сил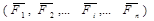

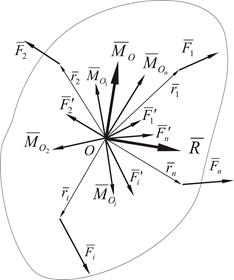
Рисунок 1.15

Возьмем какую-либо точку О за центр приведения и, пользуясь теоремой о параллельном переносе силы, перенесем все силы в эту точку, присоединяя при этом соответствующие пары. На тело теперь действует система сил , 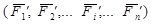, приложенных в точке О, и система пар сил, векторные моменты которых 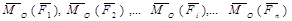. При этом .

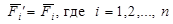Силы, приложенные в точке О, заменяются одной силой, которая является главным вектором системы сил

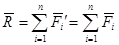(1.10)

Систему пар сил можно заменить одной парой, момент которой является главным моментом системы сил

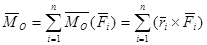(1.11)

Главный вектор системы сил не зависит от центра приведения. Он вычисляется по такой же формуле, что и равнодействующая, но при этом не эквивалентен данной системе сил.

Главный момент системы сил зависит от центра приведения.

Таким образом любую систему сил действующих на тело, можно привести к силе , равной главному вектору системы сил, и паре сил, векторный момент которой равен главному моменту системы сил относительно центра приведения.