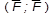Основные виды нагрузок
В задачах курса теоретической механики встречаются следующие основные виды нагрузок (активных сил): сосредоточенные силы, распределенные нагрузки, нагрузки парой сил.
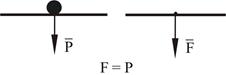
|
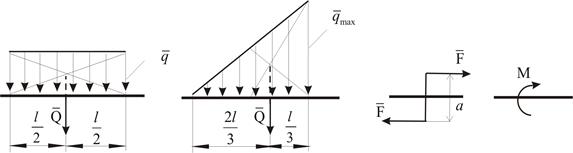
Q=ql 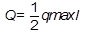 M (F)= - F×а
M (F)= - F×а
|
|
| ||||||
|
Сосредоточенные силы – силы считаются приложенными к одной точке поверхности.
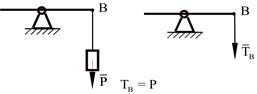
Действие груза заменяется силой, равной весу груза и прикладывается в точке его приложения к твердому телу (рис.1.7,а). В случае наложения нагрузки через гибкую связь (нить), связь и груз заменяются силой натяжения связи (нити), равной весу груза.
Распределенные нагрузки – нагрузки, которые действуют на некотором участке площади или линии поверхности тела. Распределенные нагрузки характеризуются интенсивностью 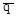 , то есть силой, отнесенной к единице длины или площади.
, то есть силой, отнесенной к единице длины или площади.
Равномерно-распределенная нагрузка имеет одинаковую интенсивность по всему участку приложения (рис.1.7, б).
Распределенную нагрузку при решении задач следует заменить сосредоточенной силой, направленной параллельно заданной нагрузке в сторону ее действия. Величина сосредоточенной силы численно равна площади эпюры распределения нагрузки, а точка приложения находится под центром тяжести площади этой эпюры (рис.1.7, б, в).
Нагрузка парой сил – нагрузка системой двух равных по модулю, параллельных и противоположно направленных сил (рис.1.7, г). Пару сил заменяют алгебраическим моментом, показывая его направление.
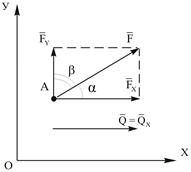
Проекция силы на ось.Если дана сила 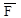 (рис.1.8), то ее можно разложить на составляющие по координатным осям Ох и Оу:
(рис.1.8), то ее можно разложить на составляющие по координатным осям Ох и Оу:
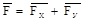 , (1.1)
, (1.1)
где 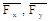 – составляющие силы
– составляющие силы 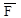 по координатным осям.
по координатным осям.
Составляющие силы по координатным осям - величины векторные.
|
Проекция силы на ось – алгебраическая величина, равная произведению модуля силы на косинус угла между направлением силы и положительным направлением оси:
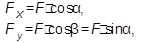 (1.2)
(1.2)
где α – угол, который образует сила 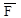 с положительным направлением осей Ох и Оу;
с положительным направлением осей Ох и Оу;
Fх , Fу – проекции силы 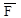 на координатные оси Ох и Оу.
на координатные оси Ох и Оу.
Если угол острый - проекция положительна, если тупой – отрицательна, а если сила перпендикулярна оси, ее проекция на ось равна нулю. Модуль силы равен:
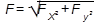 . (1.3)
. (1.3)
Проекция силы на ось положительна, если соответствующая составляющая силы направлена в положительную сторону оси, и отрицательна, если составляющая силы направлена в обратную сторону. Проекция силы на ось равна по модулю самой силе, если сила параллельна оси, и равна нулю, если сила перпендикулярна оси. Например, проекция силы 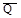 на ось Ох равна самой силе
на ось Ох равна самой силе 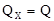 , а на ось Оу сила проецируется в точку, т.е. эта ее проекция равна нулю
, а на ось Оу сила проецируется в точку, т.е. эта ее проекция равна нулю 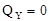 (рис.1.8). При решении задач рекомендуется вычислять абсолютное значение проекции силы как произведение модуля силы на косинус острого угла между линией действия силы и осью, определяя знак проекции по чертежу.
(рис.1.8). При решении задач рекомендуется вычислять абсолютное значение проекции силы как произведение модуля силы на косинус острого угла между линией действия силы и осью, определяя знак проекции по чертежу.
Момент силы
Алгебраический момент силы относительно точки равен произведению модуля силы на плечо, взятому со знаком плюс или минус.
Плечо h силы относительноточки равно длине перпендикуляра, опущенного из точки на линию действия силы.
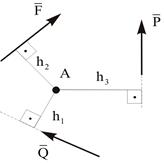
Момент силы считается положительным, если сила стремится повернуть тело относительно моментной точки против хода часовой стрелки, и отрицательным – когда по ходу часовой стрелки. Рассмотрим моменты сил 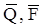 и
и 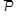 (рис.1.9).
(рис.1.9).
|
Моменты этих сил, относительно произвольной точки А, с учетом их знаков, будут равны:
M А(Q)= - Q×h1 M А(F)= - F×h2 M А(F)= -P×h3 (1.4)
где h1 , h2 , h3 – плечи сил 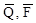 и
и 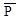 относительно точки А.
относительно точки А.
Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку.
Векторным моментом силы относительно точки называется вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относительно этой точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть, что сила стремится вращать тело против хода часовой стрелки (рис. 1.10). Плечом h силы 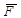 относительно точки О называется кратчайшее расстояние от этой точки до линии действия силы.
относительно точки О называется кратчайшее расстояние от этой точки до линии действия силы.
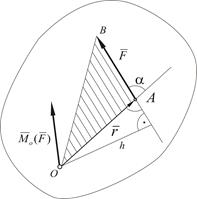
Рисунок 1.10
Таким образом , по определению, численное значение векторного момента силы 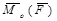 равно
равно
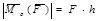 (1.5)
(1.5)
Численное значение векторного момента силы относительно точки О равно удвоенной площади треугольника, построенного на силе и моментной точке 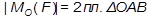
Для векторного момента силы справедлива формула
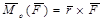 (1.6)
(1.6)
где 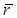 -радиус-вектор, проведенный из моментной точки в точку приложения силы.
-радиус-вектор, проведенный из моментной точки в точку приложения силы.
Моментом силы 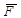 относительно оси z называют алгебраический момент проекции этой силы
относительно оси z называют алгебраический момент проекции этой силы 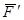 на плоскость П, перпендикулярную оси z, относительно точки пересечения оси с этой плоскостью
на плоскость П, перпендикулярную оси z, относительно точки пересечения оси с этой плоскостью
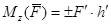 (1.7)
(1.7)
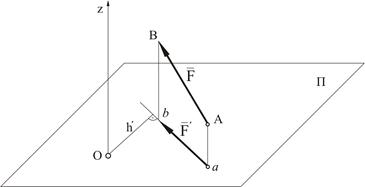
Рисунок 1.11
Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную оси стремится вращать тело вокруг положительного направления оси против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.
Из формулы (1.7) следуют свойства момента силы относительно оси:
· Момент силы относительно оси равен нулю, если сила параллельна оси, так как равна нулю проекция силы 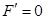 .
.
· Момент силы относительно оси равен нулю, если линия действия силы пересекает эту ось, так как равно нулю плечо проекции силы, 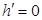 .
.
Дата добавления: 2017-06-13; просмотров: 3371;