Пара сил. Момент пары сил

Система двух равных по модулю, параллельных и противоположно направленных сил называется парой сил 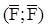. Плоскость, в которой находятся линии действия сил, называется плоскостью действия пары сил. Пара сил не имеет равнодействующей и ее силы не уравновешиваются, т.к. не лежат на одной прямой.

Алгебраический момент пары сил определяют взятым с соответствующим знаком произведением модуля одной из сил пары на плечо пары сил, т.е. на кратчайшее расстояние между линиями действия этих сил (рис.1.12):

M (F)= - F×h , M (Р)= F×d (1.8)

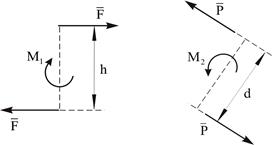
Рисунок 1.12.К моменту пары сил

Момент пары сил считают положительным, если пара сил стремится повернуть плоскость действия пары сил в сторону, противоположную направлению хода часовой стрелки, и отрицательным, если пара сил стремится повернуть плоскость в сторону направления хода часовой стрелки.

Алгебраический момент пары сил не зависит от переноса сил пары вдоль их линий действия. Действие пары сил на тело не изменится, если пару сил перенести в параллельную плоскость. У пары сил можно изменить плечо и модуль сил, сохраняя при этом алгебраический момент пары и плоскость его действия. Момент пары сил можно рассматривать как вектор (рис.1.13)

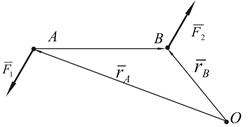
Рисунок 1.13

Векторный момент пары силесть вектор 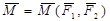, перпендикулярный плоскости действия пары, направленный в ту сторону, откуда видно, что пара сил стремится повернуть тело против хода часовой стрелки, и численно равный произведению модуля одной из сил пары на ее плечо. Векторный момент пары сил равен векторному моменту одной из ее сил относительно точки приложения другой силы или сумме векторный моментов ее сил относительно произвольной точки О. Так как выбор точки О произволен, то вектор 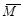можно считать приложенным в любой точке тела, то есть этот вектор свободный. Поэтому пару сил можно переносить куда угодно в плоскости и в параллельную плоскость, изменяя модуль силы и плечо пары, но сохраняя при этом неизменными модуль момента пары и направление, в котором она стремится вращать твердое тело.

Если на тело действует несколько пар сил, расположенных произвольным образом, то для их сложения и приведения к одной паре сил можно применить выражение (1.9). В самом деле, если векторные моменты пар сил равны 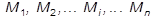, то сумма моментов всех сил, образующих эти пары, относительно какой-либо точки О равна

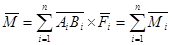(1.9)

Формула (1.9) выражает теорему о сложении пар сил.