Основные виды связей и их реакции

Основные понятия и аксиомы статики

Статика – учение о силах и условиях равновесия материальных тел, находящихся под действием сил.

Сила – мера механического взаимодействия тел. Совокупность сил, действующих на абсолютно твердое тело, называется системой сил.

Абсолютно твёрдое тело — совокупность точек, расстояния между текущими положениями которых не изменяются, каким бы воздействиям данное тело ни подвергалось.

В статике решаются две задачи:

1. Сложение сил и приведение систем сил, действующих на тело к простейшему виду;

2. Определение условий равновесия действующих на тело систем сил.

Две системы сил называются эквивалентными, если они оказывают одинаковое механическое воздействие на тело.

Система сил называется уравновешенной (эквивалентной нулю), если она не изменяет механического состояния тела (то есть состояния покоя или движения по инерции).

Равнодействующей силой называется одна сила, если она существует, эквивалентная некоторой системе сил.

Силы, линии действия которых пересекаются в одной точке, называют сходящимися.

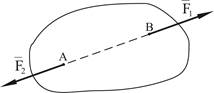
1. Аксиома о равновесии системы двух сил. Под действием двух сил, приложенных к абсолютно твердому телу, тело может находиться в равновесии тогда и только тогда, когда эти силы равны по величине и направлены вдоль одной прямой в противоположные стороны (рис. 1.1).

0

Рисунок 1.1

2. Аксиома о добавлении (отбрасывании) системы сил, эквивалентной нулю. Действие данной системы сил на абсолютно твердое тело не

изменится, если к ней прибавить или отнять уравновешенную систему сил (т.е. эквивалентную нулю).

Имеем систему 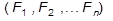; добавим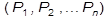 0

Получим { ; }.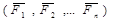

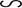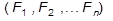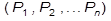Следствие: При переносе силы вдоль её линии действия, действие этой силы на тело не меняется. Из этого следствия вытекает, что сила приложенная к абсолютно твёрдому телу представляет собой скользящий вектор.

Пусть в точке А твердого тела приложена сила 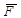(рис.1.2). К этой силе на ее линии действия в точке В в соответствии с аксиомой II добавим систему сил 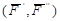, эквивалентную нулю, для которой 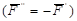. Выберем силу 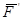, равную силе .

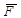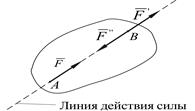
Рисунок 1.2

Полученная система трех сил 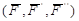эквивалентна, согласно аксиоме о добавлении равновесной системе сил, силе 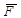, то есть .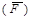

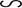
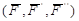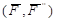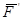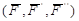
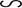
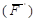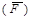
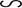
Система сил , согласно аксиоме 1, эквивалентна нулю, и согласно аксиоме 2 ее можно отбросить. Получится одна сила , приложенная в точке В, то есть . Окончательно получаем 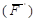. Сила 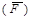приложена в точке А. Она эквивалентна такой же по модулю и направлению силе 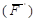, приложенной в точке В, где точка В – любая точка линии действия силы 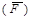. Теорема доказана: действие силы на твердое тело не изменится от переноса силы вдоль линии действия. Силу для твердого тела можно считать приложенной в любой точке линии действия, то есть сила – скользящий вектор. Как скользящий вектор сила характеризуется: численным значением (модулем) 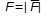; направлением силы 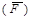; положением линии действия силы на теле.

3.Аксиома параллелограмма сил. Две силы 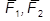, приложенные в одной точке абсолютно твердого тела, имеют равнодействующую силу 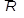, приложенную в той же точке и равную геометрической (векторной) сумме этих сил (рис.1.3).

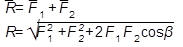
Рисунок 1.3

Следствие: Теорема о трех не параллельных силах: Если под действием трех сил тело находится в равновесии и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.

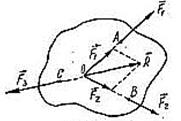
Рисунок. 1.4

Положим, что тело находится в равновесии под действием трех сил 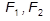, 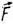₃ , приложенных в точках А, В, С (рис.1.4). По 3 аксиоме равнодействующая первых двух сил может быть найдена по правилу параллелограмма, построенного на силах 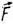₁ и 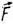_2, перенесенных вдоль линии их действия в точку О пересечения последних, т. е. 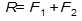. Согласно первой аксиоме статики для равновесия тела необходимо и достаточно, чтобы сила ₃ была уравновешивающей двух первых сил. Это возможно только в том случае, когда силы 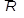и ₃ лежат на одной прямой и имеют противоположные направления. Но тогда линии действия сил 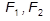, 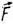₃ пересекутся в одной точке О. Любая из трех данных сил уравновешивает две другие. Выведенное условие равновесия трех не параллельных сил является необходимым, но не достаточным. Если линии действия трех сил пересекаются в одной точке, то отсюда вовсе не следует, что эти три силы представляют собой уравновешенную систему сил.

4. Аксиома о равенстве сил действия и противодействия. При всяком действии одного тела на другое имеет место такое же численно, но противоположное по направлению противодействие (III закон Ньютона). Силы взаимодействия двух тел не составляют систему уравновешенных сил, так как приложены к разным телам.

Рисунок 1.5

5. Аксиома о связях. Материальные объекты (тела и точки), которые ограничивают свободу перемещения рассматриваемого твердого тела, называются связями. Сила, с которой связь действует на тело, препятствуя его перемещению, называется реакцией связи. Реакция связи направлена противоположно возможному перемещению тела. Аксиома связей утверждает, что всякую связь можно отбросить и заменить силой или системой сил (в общем случае), то есть реакциями связи.

6. Аксиома затвердевания. Равновесие деформируемого тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым). Если деформируемое тело находилось в равновесии, то оно будет находиться в равновесии и после его затвердевания.

Основные виды связей и их реакции

Приведем примеры связей для плоской системы сил и их замены силами реакций связей.

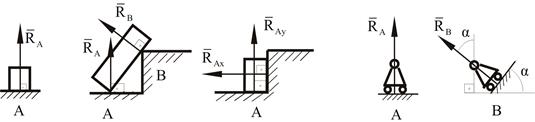
1. Гладкая поверхность (рис.1.6,а). Если тело опирается на идеально гладкую поверхность, то реакция поверхности направлена по нормали к общей касательной поверхностей тел в точке соприкосновения.

2. Подвижная шарнирная опора, подвижный шарнир – опора, поставленная на катки, не препятствующие перемещению тела параллельно опорной плоскости. Реакция подвижного шарнира направлена по нормали к поверхности, на которую опираются катки шарнира (рис.1.6,б).

	а)		б)

		г)
		в)
				д)
					е)
	Рисунок 1.6. Некоторые виды связей и их реакции а) гладкая поверхность, б) подвижная шарнирная опора, в) неподвижная шарнирная опора, г) жесткая заделка, д) стержень, е) гибкая связь

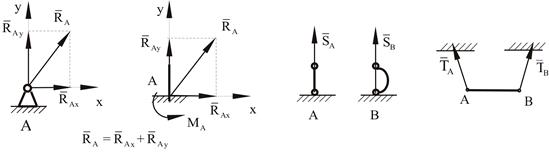
3. Неподвижная шарнирная опора, неподвижный шарнир – совокупность неподвижного валика и надетой на него втулки с твердым телом, вращающимся вокруг оси (подшипник, петля). Реакция неподвижного шарнира проходит через ось валика, в неизвестном направлении, поэтому определяют две ее составляющие, направленные параллельно осям координат, перпендикулярных оси валика (рис. 1.6, в).

4. Жесткая заделка – жестко закрепленная балка, стержень. Связь препятствует любому движению конца балки. Для определения реакции жесткой заделки необходимо определить составляющие главного вектора R_А, направленные параллельно осям координат и главный момент М_А заделки (рис. 1.6, г).

5. Стержень – жесткий невесомый стержень, концы которого соединены с другими частями конструкции шарнирами. Реакция направлена по линии, проведенной через опорные шарниры стержня (рис. 1.6, д).

6. Гибкая связь – нить, цепь, трос. Реакция приложена к твердому телу в точке соприкосновения и направлена по связи (рис. 1.6, е).