Возбужденные состояния ядер
Возбуждение ядра – сообщение ядру дополнительной энергии, в результате чего увеличивается его внутренняя энергия, и ядро переходит из основного состояния в возбужденное. Ядро является квантовой системой взаимодействующих нуклонов и имеет строго определенный и дискретный набор разрешенных энергетических состояний. Наименьшее количество энергии, которое может поглотить ядро, соответствует его первому возбужденному уровню. Уровни возбуждения бывают одночастичными и коллективными. Возбуждение легких ядер на нижние энергетические уровни обусловлены переходом одного из нуклона в ближайшее незанятое состояние с большей энергией. Такие уровни называются одночастичными. Для тяжелых ядер переход на нижние уровни возбуждения обусловлен обычно вращением ядра (несферические ядра (см. §1.6.3) могут вращаться), а на более высокие уровни связан с возбуждением периодических колебаний плотности ядра (без изменения формы) или же с колебанием формы ядра. Уровни подобного свойства называются коллективными, так как вызваны коллективным взаимодействием нуклонов в ядре. Многие из уровней имеют сложную смешанную природу.
На рис.1.7.1 изображены типичные схемы возбужденных уровней легкого и тяжелого ядер. Система энергетических уровней ядра называется энергетическим спектром ядра. Энергия каждого уровня обозначается слева, а спин и четность (см. §1.8) данного состояния справа. Совокупность значений этих величин называется ха 
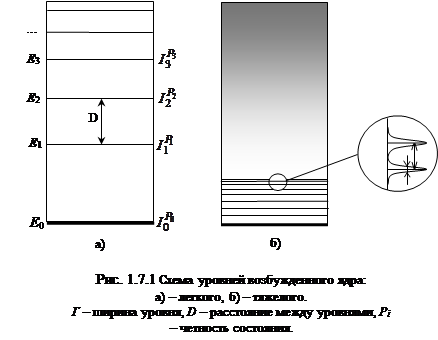 рактеристикой уровня. Первый возбужденный уровень E1 легких ядер (А < 50) расположен при энергии ~ 1 МэВ, у тяжелых (А > 200) ~ 0,1 МэВ. Спины ядер в возбужденных состояниях могут отличаться от спинов в основном состоянии, поскольку спин ядра зависит не только от спина нуклонов но и от их внутреннего движения (орбитальных моментов).
рактеристикой уровня. Первый возбужденный уровень E1 легких ядер (А < 50) расположен при энергии ~ 1 МэВ, у тяжелых (А > 200) ~ 0,1 МэВ. Спины ядер в возбужденных состояниях могут отличаться от спинов в основном состоянии, поскольку спин ядра зависит не только от спина нуклонов но и от их внутреннего движения (орбитальных моментов).
Все возбужденные уровни не являются строго моноэнергетическими, а имеют конечную ширину Г, которая связана со средним временем t жизни ядра в данном возбужденном состоянии соотношением неопределенностей:
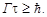
| (1.7.1) |
Типичная величина t ~ 10-14 с. Этому значению t соответствует Г ~ 0,1 эВ. Однако бывают величины t и Г на много отличающиеся от этих. Следует подчеркнуть, что среднее время жизни ядра в возбужденном состоянии велико по сравнению с характерным временем ядерного взаимодействия (~ 10-23 с, см. (1.9.17)), то есть по ядерным масштабам возбужденное ядро живет весьма долго.
На рис. 1.7.1 (в кружке) показана в увеличенном виде структура отдельных уровней. Распределение W(E) представляет собой плотность вероятности образования возбужденного состояния ядра от энергии. Ширина уровня Г определяется на половине высоты этого распределения.
Понятие уровня, а тем самым и его характеристики, имеют смысл до тех пор, пока ширина Г уровня не превышает расстояния D между соседними уровнями, т.е. пока уровни не перекрываются. Поэтому условие существования уровня имеет следующий вид:
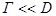 . .
| (1.7.2) |
При выполнении условия (1.7.2) характеристики стабильных ядер можно вводить и для нестабильных ядер, а также для стабильных ядер, находящихся в возбужденном состоянии.
С ростом энергии возбуждения расстояние между уровнями в среднем экспоненциально уменьшается. Одновременно уменьшается среднее время жизни τ ядра на данном уровне и в соответствии с (1.7.1) растет ширина уровней Г . В результате при некоторых значениях энергии возбуждения ширина уровней становится сравнимой с расстоянием между соседними уровнями и при дальнейшем увеличении энергии возбуждения уровни сольются, а энергетический спектр ядра в этой области энергий становится сплошным (непрерывным). Для тесно расположенных уровней можно говорить оплотности уровней - числе уровней, приходящихся на единичный интервал энергии.
Если энергия возбуждения ядра меньше энергии связи нуклона, то переход в основное состояние происходит с испусканием g-кванта, или последовательного каскада g-квантов, которые уносят из ядра энергию возбуждения. Так как интенсивность электромагнитных сил (см. §1.9 п.3) много меньше ядерных, то и процессы под их действием протекают существенно медленнее. Поэтому, если энергия возбуждения превышает энергию отделения нуклона, то переход в основное состояние будет происходить преимущественно с испусканием нуклона (чаще всего нейтрона, так как для него отсутствует кулоновский барьер). При этом надо помнить, что возникающее конечное ядро не имеет ничего общего с начальным ядром.
Четность
Поведение изолированных физических систем со временем характеризуются рядом всеобщих законов, таких как законы сохранения энергии, импульса и момента импульса. Совокупность этих законов называют интегралами движения. Законы сохранения являются отражением свойств симметрии пространства-времени (мира), в которых движутся тела. Например, сохранение энергии есть следствие однородности времени, то есть неизменности (инвариантности) физических законов относительно изменения начала отсчета времени. Сохранение импульса есть следствие однородности пространства, то есть инвариантности физических законов относительно параллельного переноса декартовых координат. Закон сохранения момента импульса - следствие изотропности пространства, то есть инвариантности физических законов относительно поворота системы координат.
Имеется еще один вид симметрии пространства-времени, связанный с пространственной инверсией. Инверсия, или просранственное отражение, есть изменение направления (знаков) всех трех пространственных осей координат:
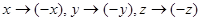
| (1.8.1) |
В результате инверсии правовинтовая система координат преобразуется в левовинтовую и наоборот. В сферической системе координат инверсия выглядит следующим образом:
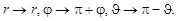
| (1.8.2) |
При определенных условиях микроскопическая частица характеризуется свойством, которому, в отличие от энергии, импульса или момента импульса не отвечет никакой классический аналог в макромире. Это свойство непосредственно относится к волновой функции частицы и связано с ее поведением при инверсии системы координат. Согласно основному физическому свойству волновой функции, квадрат ее модуля 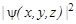 определяет плотность вероятности найти микрочастицу в фиксированный момент времени в данной точке пространства. Очевидно, что плотность вероятности не должна зависеть от того, в какой системе координат – правовинтовой (x, y, z) или левовинтовой (-x, -y, -z) выполняются наблюдения:
определяет плотность вероятности найти микрочастицу в фиксированный момент времени в данной точке пространства. Очевидно, что плотность вероятности не должна зависеть от того, в какой системе координат – правовинтовой (x, y, z) или левовинтовой (-x, -y, -z) выполняются наблюдения:
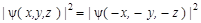 ; ;
| (1.8.3) |
или в сферической системе координат:
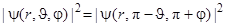 , ,
| (1.8.4) |
если угол 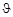 откладывается относительно оси Z, направление которой совпадает с одной из векторных характеристик, определяющих неоднородность пространства, например с вектором напряженности магнитного поля. Для зеркально-симметричного процесса вероятности вылета из ядра какой-либо частицы под углами
откладывается относительно оси Z, направление которой совпадает с одной из векторных характеристик, определяющих неоднородность пространства, например с вектором напряженности магнитного поля. Для зеркально-симметричного процесса вероятности вылета из ядра какой-либо частицы под углами 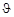 и
и 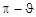 относительно направления спина ядра должны быть равны. Таким образом, для зеркально симметричного процесса абсолютная величина ψ-функции не изменяется
относительно направления спина ядра должны быть равны. Таким образом, для зеркально симметричного процесса абсолютная величина ψ-функции не изменяется
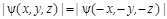 . .
| (1.8.5) |
В общем случае операция инверсии ведет к умножению ψ-функции на некоторое число Р:
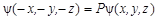 . .
| (1.8.6) |
Применим к выражению (1.8.6) операцию инверсии еще раз:
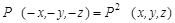 . .
| (1.8.7) |
Полученная таким образом функция P2 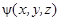 должна совпадать с первоначальной функцией
должна совпадать с первоначальной функцией 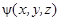 . Следовательно устанавливаем, что Р2 = 1, а Р = ± 1. Величина Р (parity – четность) называется четностью и является еще одним квантовым числом. Таким образом, операция инверсии либо оставляет функцию
. Следовательно устанавливаем, что Р2 = 1, а Р = ± 1. Величина Р (parity – четность) называется четностью и является еще одним квантовым числом. Таким образом, операция инверсии либо оставляет функцию 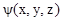 неизменной, либо изменяет знак функции на обратный:
неизменной, либо изменяет знак функции на обратный:
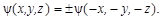
| (1.8.8) |
Поведение функции 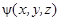 при инверсии координат, зависит от внутренних свойств частицы, описываемой этой функцией. Каждая частица с ненулевой массой покоя обладает особым свойством, которое называется внутренней (или собственной) четностью. Если Р = +1, то говорят, что частица имеет положительную внутреннюю четность. Если же Р = -1, то частица имеет отрицательную внутреннюю четность. Внутренняя четность протона, нейтрона и электрона принимается положительной, т.е. для них Р = +1.
при инверсии координат, зависит от внутренних свойств частицы, описываемой этой функцией. Каждая частица с ненулевой массой покоя обладает особым свойством, которое называется внутренней (или собственной) четностью. Если Р = +1, то говорят, что частица имеет положительную внутреннюю четность. Если же Р = -1, то частица имеет отрицательную внутреннюю четность. Внутренняя четность протона, нейтрона и электрона принимается положительной, т.е. для них Р = +1.
Частицы могут совершать орбитальное движение, характеризуемое квантовыми числами l, и обладать орбитальной четностью (‑1)l. Полная четность микрочастицы с внутренней четностью Р равна Р(‑1)l.
Полная четность П системы, состоящей из k частиц определяется произведением полных четностей отдельных частиц:
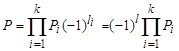 , ,
| (1.8.9) |
где l = l1+ l2+. . . + lk – суммарный относительный орбитальный момент системы. Так как внутренняя четность протона, нейтрона и электрона равна +1, то из (1.8.9) для систем из этих частиц получаем
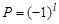 . .
| (1.8.10) |
Замечательным свойством для многих изолированных квантовых систем является закон сохранение четности: если изолированная физическая система в момент времени t = 0 имела определенную четность, то система сохраняет свою четность во все последующие моменты времени. Таким образом, четность является таким же интегралом движения, как энергия, импульс или момент импульса. Установлено, что при переходах из одного состояния в другое четность сохраняется в процессах, обусловленных сильными (с участием ядерных сил) и электромагнитными взаимодействиями. В противоположность этому в результате слабого взаимодействия (см. §3.5) четность системы не сохраняется.
Выполнение закона сохранения четности приводит к правилам отбора для электромагнитного излучения атомов и ядер, для радиоактивных превращений ядер и ядерных реакций.
Основные состояния четно-четных ядер всегда имеют положительную четность. У других ядер основные состояния могут быть как четными, так и нечетными. Четность отмечается знаком плюс или минус при обозначении спина - IP (например, 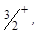 1- и т.п.). Ядра в возбужденных состояниях могут иметь различную четность, не обязательно совпадающую с четностью основного состояния.
1- и т.п.). Ядра в возбужденных состояниях могут иметь различную четность, не обязательно совпадающую с четностью основного состояния.
Ядерные силы
Ядерные силы относятся к так называемым сильным взаимодействиям и существенно отличаются по своим свойствам от электромагнитных и гравитационных. В полной мере природа ядерных сил до настоящего времени не выяснена. Даже для простейшей системы из двух нуклонов неизвестна зависимость ядерных сил от расстояния между нуклонами. Многообразие свойств ядерных сил по сравнению с электромагнитными не позволяют создать законченную теорию, подобную квантовой электродинамики для расчета свойств атомов.
Перечислим основные свойства ядерных сил и укажем на экспериментальные факты, подтверждающие эти свойства.
 1. Огромная энергия связи нуклонов в ядре свидетельствует о том, что между нуклонами действуют силы притяжения, что подтверждается существованием стабильных ядер. Эти силы самые интенсивные в природе. Например, энергия связи простейшего ядра - 4Не - составляет 2,22 МэВ, а для простейшего атома – водорода – равна 13,6 эВ.
1. Огромная энергия связи нуклонов в ядре свидетельствует о том, что между нуклонами действуют силы притяжения, что подтверждается существованием стабильных ядер. Эти силы самые интенсивные в природе. Например, энергия связи простейшего ядра - 4Не - составляет 2,22 МэВ, а для простейшего атома – водорода – равна 13,6 эВ.
2. Уже первые опыты Резерфорда показали, что ядерные силы – короткодействующие. Это свойство ядерных сил подтверждается многочисленными данными по измерению размеров атомных ядер. Ядерные силы удерживают нуклоны на расстояниях ~ (1,2 ÷ 1,4) ·10‑13 см. При расстояниях между нуклонами, превышающих 2·10‑13 см действие ядерных сил не обнаруживается, тогда как на расстояниях меньших 1·10‑13 см, притяжение нуклонов заменяется отталкиванием.
3. На расстояниях, где между протонами действуют ядерные силы притяжения, они превосходят кулоновские силы отталкивания приблизительно в 100 раз, действие которых на этих расстояниях также очень велико. Короткодействие ядерных сил приводит к резкому разграничению областей, где действуют только дальнодействующие кулоновские силы, или только ядерные, которые подавляют кулоновские силы на малых расстояниях. На рис.1.9.1а показана потенциальная энергия взаимодействия протона с тремя различными ядрами: легким ( 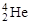 ), средним (
), средним ( 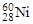 )и тяжелым (
)и тяжелым ( 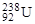 ). Функции U(r) представляют собой энергию взаимодействия между протоном и ядром. За границами ядра существует только кулоновское отталкивание, энергия которого равна
). Функции U(r) представляют собой энергию взаимодействия между протоном и ядром. За границами ядра существует только кулоновское отталкивание, энергия которого равна
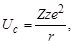
| (1.9.1) |
где Z – заряд ядра, z - заряд налетающей частицы. В области, где начинает проявляться действие ядерных силы притяжения, потенциальная энергия круто падает на расстояниях ~ 10-13 см, что соответствует большой интенсивности ядерных сил (сила пропорциональна антиградиенту потенциальной энергии - dU/dr). Внутри ядра потенциальная энергия отрицательна (см. рис. 1.4.1) и представлена некоторой средней величиной (дно потенциальной ямы). На рисунке 1.9.1а пунктиром показаны также удельные энергии связи рассматриваемых ядер. Радиусы ядер на этом же рисунке подсчитаны по формуле (1.5.2). Энергия ядерного взаимодействия на рисунке 1.9.1а характеризует только центрально-симметричную часть ядерных сил и не учитывает зависимость ядерных сил от спина (см. ниже п.4) и нецентральный характер ядерных сил (см. ниже п.7). Таким образом, заряженная частица для сближения с ядром или при вылете из ядра должна преодолеть кулоновский барьер. На рис. 1.9.1б приведена модельная потенциальная функция взаимодействия между ядром и заряженной частицей, представленной в виде точечного заряда. Высота кулоновского барьера в этом случае составит
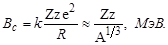
| (1.9.2) |
Ядерное взаимодействие между ядром и частицей аппроксимируется отвесной линией. Нейтроны не имеют электрического заряда и потому беспрепятственно сближаются с ядрами, т.е. для них отсутствует кулоновский барьер (жирная горизонтальная линия на рис. 1.9.1б в области r > R). Ядерный потенциал у нейтрона оказывается таким же (с точностью до различия в массах), как и у протона (см. ниже п.5).
4. Ядерные силы зависят от взаимной ориентации спинов взаимодействующих нуклонов и от взаимной ориентации орбитального и спинового моментов каждого из нуклонов. Это означает, что внутри ядра следует учитывать спин-орбитальное взаимодействие нуклонов. Зависимость ядерных сил от спина хорошо видна на примере дейтона, который имеет спин, равный единице, т.е. нейтрон и протон могут существовать в связанном состоянии только при параллельных спинах. При антипараллельных спинах нейтрон и протон не образует связанной системы, но притяжение между ними все же существует, что приводит к значительной эффективности рассеяния нейтронов на протонах. Поэтому рассеяние нейтронов на водородосодержащих средах оказывается также эффективным и широко используется для замедления нейтронов в ядерных реакторах.
Если нуклоны одноименные, то наибольшее притяжение между ними наблюдается в случае антипараллельной ориентации их спинов, а для разноименных нуклонов – в случае параллельной ориентации спинов. Как раз этой особенностью объясняется эффект спаривания нуклонов (см. §1.4 п.3).
 5. Интенсивность ядерного взаимодействия не зависит от электрического заряда нуклонов. Ядерные силы, действующие между двумя протонами (р – р), протоном и нейтроном (р – n) и двумя нейтронами (n – n), находящихся в одинаковых пространственных и спиновых состояниях, одинаковы по величине. Это свойство называется зарядовой независимостью ядерных сил. Другими словами, протон и нейтрон оказываются равноправными относительно ядерного взаимодействия. Это, конечно, не означает, что взаимное кулоновское отталкивание протонов не играет роли внутри ядра или при рассеянии двух свободных протонов. На рис. 1.9.2 изображена схема энергетических уровней двух зеркальных ядер
5. Интенсивность ядерного взаимодействия не зависит от электрического заряда нуклонов. Ядерные силы, действующие между двумя протонами (р – р), протоном и нейтроном (р – n) и двумя нейтронами (n – n), находящихся в одинаковых пространственных и спиновых состояниях, одинаковы по величине. Это свойство называется зарядовой независимостью ядерных сил. Другими словами, протон и нейтрон оказываются равноправными относительно ядерного взаимодействия. Это, конечно, не означает, что взаимное кулоновское отталкивание протонов не играет роли внутри ядра или при рассеянии двух свободных протонов. На рис. 1.9.2 изображена схема энергетических уровней двух зеркальных ядер 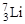 и
и 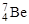 . Зеркальными называются ядра изобаров, количество протонов в одном из которых равно количеству нейтронов в другом и наоборот. В зеркальных ядрах число (р – n) связей остается постоянным, а (р – р) связи заменены на (n – n) связи. Энергии основных состояний у них сдвинуты друг относительно друга на величину разности ΔUкул кулоновской энергии ядер и разность Δmнук нуклонов (mn > mp)
. Зеркальными называются ядра изобаров, количество протонов в одном из которых равно количеству нейтронов в другом и наоборот. В зеркальных ядрах число (р – n) связей остается постоянным, а (р – р) связи заменены на (n – n) связи. Энергии основных состояний у них сдвинуты друг относительно друга на величину разности ΔUкул кулоновской энергии ядер и разность Δmнук нуклонов (mn > mp)
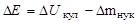
| (1.9.3) |
Из рисунка видно, что соответствующие уровни энергии (энергетические спектры ядер) очень близки, а спины и четности уровней совпадают. Однако, строго говоря, приведенная информация не является прямым доказательством зарядовой независимости ядерных сил, так как сопоставляются не процессы парных взаимодействий между нуклонами отдельных типов, а рассматриваются свойства сложных нуклонных систем. Непосредственное доказательство гипотезы о зарядовой независимости ядерных сил получено в прямых опытах по изучению (р – р) и (n – р) рассеяния.
6. Постоянство средней энергии связи на нуклон (рис. 1.4.2) указывает на свойство насыщения ядерных сил. Это означает, что каждый нуклон в ядре взаимодействует с ограниченным числом соседних нуклонов. Свойство насыщения ядерных сил имеет парный характер. Например, пара нейтронов и пара протонов образует одно из самых прочных легких ядер 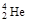 - a-частицу. Присоединение одного нейтрона к a-частице образует нестабильное ядро
- a-частицу. Присоединение одного нейтрона к a-частице образует нестабильное ядро 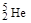 , а присоединение одного протона – нестабильное ядро
, а присоединение одного протона – нестабильное ядро 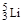 .
.
7. Ядерные силы имеют нецентральный характер. Центральными называются силы, которые действуют вдоль прямой, соединяющей центры инерции взаимодействующих тел. Центральные силы могут зависеть от относительной ориентации спинов частиц, но не должны зависеть от ориентации спинов относительно линии, соединяющей центры инерции частиц. Рассмотрим некоторые свойства простейшего ядра 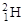 , которое имеет такое же значение в ядерной физике, как атом водорода - в атомной физике. Спины нейтрона и протона в дейтоне параллельны (см. п.4), поэтому магнитный момент дейтона должен определяться алгебраической сумме магнитных моментов протона и нейтрона, равной μd + μd = 2,79 – 1,91 = 0,88. Измеренное значение магнитного момента дейтона μd = 0,86 (см. таблицу 1.6.1) немного отличается, хотя величина расхождения намного превышает точность измерений. Различие можно объяснить только наличием у протона орбитального момента. Дейтон имеет квадрупольный момент +0,0028·10‑24 см2 (таблица 1.6.2), т.е. распределение плотности электрического заряда (а следовательно и ядерного вещества) отлично от сферически симметричного и вытянуто вдоль спина. Таким образом, система из протона и нейтрона имеет наибольшую энергию связи только тогда, когда спины обоих нуклонов направлены вдоль оси дейтона. Это свидетельствует о том, что ядерные силы в общем случае имеют нецентральный характер, так как они зависят не только от расстояния между нуклонами, но и от ориентации спинов относительно линии, соединяющей нуклоны. Макроскопическим аналогом такого явления служит характер взаимодействия между двумя
, которое имеет такое же значение в ядерной физике, как атом водорода - в атомной физике. Спины нейтрона и протона в дейтоне параллельны (см. п.4), поэтому магнитный момент дейтона должен определяться алгебраической сумме магнитных моментов протона и нейтрона, равной μd + μd = 2,79 – 1,91 = 0,88. Измеренное значение магнитного момента дейтона μd = 0,86 (см. таблицу 1.6.1) немного отличается, хотя величина расхождения намного превышает точность измерений. Различие можно объяснить только наличием у протона орбитального момента. Дейтон имеет квадрупольный момент +0,0028·10‑24 см2 (таблица 1.6.2), т.е. распределение плотности электрического заряда (а следовательно и ядерного вещества) отлично от сферически симметричного и вытянуто вдоль спина. Таким образом, система из протона и нейтрона имеет наибольшую энергию связи только тогда, когда спины обоих нуклонов направлены вдоль оси дейтона. Это свидетельствует о том, что ядерные силы в общем случае имеют нецентральный характер, так как они зависят не только от расстояния между нуклонами, но и от ориентации спинов относительно линии, соединяющей нуклоны. Макроскопическим аналогом такого явления служит характер взаимодействия между двумя 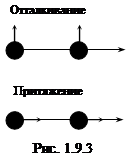 одинаково намагниченными шариками (рис. 1.9.3). При параллельных векторах магнитной индукции каждого из шариков между ними могут действовать как силы притяжения, так и отталкивания, в зависимости от ориентации векторов магнитной индукции относительно вектора, проходящего через центры инерции шариков.
одинаково намагниченными шариками (рис. 1.9.3). При параллельных векторах магнитной индукции каждого из шариков между ними могут действовать как силы притяжения, так и отталкивания, в зависимости от ориентации векторов магнитной индукции относительно вектора, проходящего через центры инерции шариков.
8. Ядерные силы имеют обменный характер. Это означает, что взаимодействие между двумя нуклонами вызвано обменом третьей частицей - пи-мезоном. Такую гипотезу высказали в 1934 г. И. Тамм и в 1935 г. Х. Юкава по аналогии с представлением о взаимодействии между электрическими зарядами, принятым в квантовой электродинамике. Взаимодействие между зарядами осуществляется через электромагнитное поле, которое может быть представлено как совокупность квантов энергии – фотонов. Каждый заряд создает вокруг себя поле, непрерывно испуская и поглощая фотоны. Процесс взаимодействия между двумя зарядами заключается в обмене виртуальными, а не реальными фотонами. В квантовой механике виртуальными называются частицы, которые не могут быть обнаружены за время их существования. Рассмотрим на примере покоящегося электрона процесс создания им в окружающем пространстве электрического поля:
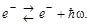
| (1.9.4) |
Превращение, описываемое уравнением (1.9.4), сопровождается нарушением закона сохранения энергии:
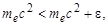
| (1.9.5) |
где 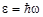 - энергия виртуального фотона. Изменение энергии системы
- энергия виртуального фотона. Изменение энергии системы 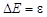 должно удовлетворять квантовомеханическому соотношению неопределенностей:
должно удовлетворять квантовомеханическому соотношению неопределенностей:
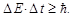
| (1.9.6) |
Если до истечения времени
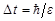
| (1.9.7) |
виртуальный фотон будет поглощен этим же или другим электроном, то нарушение закона сохранения энергии не может быть обнаружено. Если же электрону сообщить дополнительную энергию (от электрического поля или при соударении с другим зарядом), то может быть испущен реальный фотон, время существования которого неограниченно.
За время 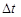 виртуальный фотон может передать взаимодействие между точками, разделенных расстоянием
виртуальный фотон может передать взаимодействие между точками, разделенных расстоянием
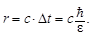
| (1.9.8) |
Так как энергия виртуального фотона 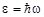 может быть сколь угодно мала (если
может быть сколь угодно мала (если 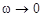 ), то радиус действия электромагнитных сил неограничен. Однако, если энергия покоя виртуальной частицы отлична от нуля, то радиус взаимодействия соответствующих сил будет ограничен величиной (предполагая, что ее скорость
), то радиус действия электромагнитных сил неограничен. Однако, если энергия покоя виртуальной частицы отлична от нуля, то радиус взаимодействия соответствующих сил будет ограничен величиной (предполагая, что ее скорость 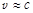 )
)
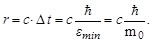
| (1.9.9) |
Полагая в (1.9.9) радиус r действия ядерных сил равным 1,3·10-13 см, получим, что кванты поля ядерных сил должны иметь массу покоя 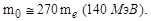 Таким образом, для образования свободных (не виртуальных) квантов ядерного поля необходима энергия не менее 140 Мэв. Эти частицы были впоследствии открыты в составе космических лучей (1947 г., Оккиалини и Поуэлл) и были названы π-мезонами (пионами).
Таким образом, для образования свободных (не виртуальных) квантов ядерного поля необходима энергия не менее 140 Мэв. Эти частицы были впоследствии открыты в составе космических лучей (1947 г., Оккиалини и Поуэлл) и были названы π-мезонами (пионами).
Существует три типа пионов - положительный пион (π+) с зарядом +е, отрицательный (π-) с зарядом -е и нейтральный (π0). Все три частицы нестабильны. Заряженные пионы имеют одинаковую массу, равную 273mе (140 МэВ), и время жизни τ = 2,55·10-8 с. Масса нейтрального пиона составляет 264mе (135 МэВ), а время жизни τ = 2,1·10-16 с. Спин любого из пиона равен нулю.
В результате аналогичных (1.9.4) виртуальных процессов
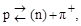
| (1.9.10) |
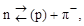
| (1.9.11) |
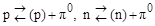
| (1.9.12) |
нуклон оказывается окруженным облаком виртуальных π-мезонов, которые образуют поле ядерных сил. Поглощение этих пионов другими нуклонами приводит к сильному взаимодействию между нуклонами и происходит по одной из следующих схем:
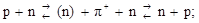
| (1.9.13) |
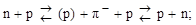
| (1.9.14) |
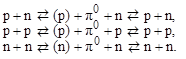
| (1.9.15) |
Процесс (1.9.13) находит экспериментальное подтверждение в рассеянии нейтронов на протонах. После прохождения пучка нейтронов через мишень, содержащую ядра 1Н, в пучке появляются протоны, которые имеют ту же энергию и направление движения, что и падающие нейтроны. Количество таких протонов намного превышает возможность образования протонов в результате упругого взаимодействия нейтронов с протонами мишени. Соответствующее количество нейтронов обнаруживается и в мишени. Остается признать, что часть нейтронов, пролетая вблизи ядер 1Н захватывает виртуальные π+-мезоны и превращается в протоны.
Орбитальное движение π --мезонов в виртуальном процессе (1.9.11) вызывает возникновение у нейтрона отрицательного магнитного момента (см. таб. 1.6.1), так как нейтрон часть времени проводит в виртуальном состоянии 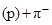 . Аномальный магнитный момент протона (
. Аномальный магнитный момент протона ( 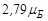 вместо одного ядерного магнетона, см. §1.6 п.2) можно также объяснить орбитальным движением π+-мезонов в течение того времени, когда протон находится в виртуальном состоянии (1.9.10).
вместо одного ядерного магнетона, см. §1.6 п.2) можно также объяснить орбитальным движением π+-мезонов в течение того времени, когда протон находится в виртуальном состоянии (1.9.10).
Оценим время виртуального процесса как
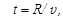
| (1.9.16) |
где 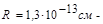 радиус действия ядерных сил, а v - скорость пиона. Полагая кинетическую энергию пиона равной средней энергии связи нуклона в ядре
радиус действия ядерных сил, а v - скорость пиона. Полагая кинетическую энергию пиона равной средней энергии связи нуклона в ядре 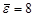 МэВ, получим
МэВ, получим
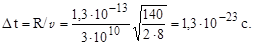
| (1.9.17) |
Эту величину часто называют характерным временем ядерного взаимодействия.
В рамках обменной теории оказывается маловероятным обмен пионами между одним и двумя другими нуклонами, находящимися в пределе радиуса действия ядерных сил. Отсюда вытекает свойство насыщения ядерных сил со всеми вытекающими последствиями: постоянство удельной энергии связи, рост объема ядра пропорционально числу частиц нуклонов в ядре, независимость потенциала от координаты внутри ядра. Мезонная теория содержит в своей основе глубокое и правильное описание природы ядерных сил, но выяснилось, что расчеты в этой теории настолько сложны, что никому еще не удалось их проделать. И до настоящего времени не существует надежных способов решения уравнений этой теории. Это является одной из причин создания большого числа разнообразных моделей ядра в ядерной физике (см. гл.2 §1).
Изотопический спин
Выше в п.5 §1.9 отмечалось свойство зарядовой независимости ядерных сил, действующих между двумя нуклонами. Гипотезу зарядовой независимости ядерных сил можно кратко выразить в виде символической записи:
| (n - n) ≡ (n – р) ≡(р – р). | (1.10.1) |
Неразличимость протона и нейтрона вне действия электромагнитных полей позволяет говорить оних как об одной частице - нуклоне, которая может быть в различных состояниях - протонном и нейтронном. Тождественность ядерных свойств нейтрона и протона (небольшое различие в массах связано с отличием от нуля электрического заряда протона) можно описать с помощью формальной, но очень удобной квантовомеханической характеристики - вектора изотопического спина 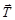 (В. Гейзенберг, 1932 г.) ядра. В отличие от спина ядра, имеющего размерность механического момента и определяемого в обычном конфигурационном пространстве, вектор изотопического спина
(В. Гейзенберг, 1932 г.) ядра. В отличие от спина ядра, имеющего размерность механического момента и определяемого в обычном конфигурационном пространстве, вектор изотопического спина 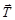 вводится в формальном изотопическом пространстве не имеющем физической размерности и имеет три компоненты Тx, Тy и Тz. Частицы с одинаковым значением изоспина, но с разными знаками электрического заряда отличаются только своей проекцией на ось Z, часто называемой третьей компонентой Т3 ≡ Тz. Семейство всех таких частиц образует мультиплет. Полагается, что
вводится в формальном изотопическом пространстве не имеющем физической размерности и имеет три компоненты Тx, Тy и Тz. Частицы с одинаковым значением изоспина, но с разными знаками электрического заряда отличаются только своей проекцией на ось Z, часто называемой третьей компонентой Т3 ≡ Тz. Семейство всех таких частиц образует мультиплет. Полагается, что 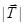 = 1/2 для обоих нуклонов. Нуклоны все время находятся только в начале системы координат изотопического пространства. Они могут только совершать поворот относительно оси X или Y, но не могут двигаться поступательно в этом пространстве. Тем самым нуклоны в изотопическом пространстве не могут иметь импульса и орбитального момента, а могут иметь только изотопический спин. В соответствии с квантовомеханическим правилом проекция изотопического спина Тz нуклона на ось Z может иметь 2Т + 1 значений, то есть две проекции. Проекция Тz = 1/2 соответствует протону, Тz = ‑1/2 - нейтрону. Итак, протон и нейтрон считаются различно ориентированными в изотопическом пространстве состояниями одной и той же частицы – нуклона. При таком рассмотрении нуклон представляет собой изотопический дублет. Так как характер ядерного взаимодействия не зависит от сорта нуклонов (т.е. от знака проекции Тz), то ядерное взаимодействие нуклона определяется только величиной вектора изотопического спина
= 1/2 для обоих нуклонов. Нуклоны все время находятся только в начале системы координат изотопического пространства. Они могут только совершать поворот относительно оси X или Y, но не могут двигаться поступательно в этом пространстве. Тем самым нуклоны в изотопическом пространстве не могут иметь импульса и орбитального момента, а могут иметь только изотопический спин. В соответствии с квантовомеханическим правилом проекция изотопического спина Тz нуклона на ось Z может иметь 2Т + 1 значений, то есть две проекции. Проекция Тz = 1/2 соответствует протону, Тz = ‑1/2 - нейтрону. Итак, протон и нейтрон считаются различно ориентированными в изотопическом пространстве состояниями одной и той же частицы – нуклона. При таком рассмотрении нуклон представляет собой изотопический дублет. Так как характер ядерного взаимодействия не зависит от сорта нуклонов (т.е. от знака проекции Тz), то ядерное взаимодействие нуклона определяется только величиной вектора изотопического спина 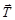 , а не его проекцией, которая определяет электрические свойства нуклона.
, а не его проекцией, которая определяет электрические свойства нуклона.
Поэтому ядерное взаимодействие инвариантно по отношению к вращению нуклона в изотопическом пространстве (например, замена протона нейтроном), так как не изменяет абсолютной величины вектора изотопического спина. Это свойство ядерных сил называется изотопической инвариантностью. Изотопическая инвариантность утверждает, что все ядерные взаимодействия (и вообще все сильные взаимодействия) инвариантны (неизменны) относительно поворота вектора изотопического спина в изотопическом пространстве, подобно тому, как инвариантны взаимодействия относительно поворота обычной конфигурационной системы координат, так как при этом не изменяется величина механического момента (закон сохранения спина, см. §1.8). Это утверждение является содержанием закона сохранения изотопического спина. Изотопический спин является такой же важной характеристикой квантовых частиц, испытывающих сильное взаимодействие, как энергия, спин и четность.
Рассмотрим систему из двух взаимодействующих между собой нуклонов. По правилам сложения квантовых моментов (1.6.8) возможны два значения суммарного вектора изотопического спина Т12 двух нуклонов
| Т12 =Т1 + Т2 , Т1 + Т2 - 1 , . . . , |T1 – T2| = =1/2 +1/2, 1/2+ 1\2 – 1 = 1, 0. | (1.10.) |
Однако в системах (n-n) и (p‑p) величина вектора суммарного спина Т12 не может быть равна нулю, а обязательно равна только единице, ибо его проекция равна единице по абсолютной величине (+1 или –1 соответственно). В системе (n-р) проекция вектора суммарного спина равна нулю и в этой связи система может находиться в состояниях с величиной вектора изотопического спина равной как нулю, так и единице. Значит, в состоянии с изотопическим спином, равным единице, система (n-р) ничем, с точки зрения ядерного взаимодействия, не отличается от систем (n-n) и (p‑p), что и постулировалось в начале этого параграфа.
Этот важный вывод будет использован в §1.11, чтобы обосновать невозможность связанных состояний (n-n), (p‑p) и (n-р) с суммарным вектором изотопического спина, равным единице.
Понятие изотопического спина можно обобщить и на основное состояние атомного ядра (A, Z). В этом случае величину и проекцию изоспина ядра можно найти по формулам:
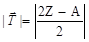 ; ; 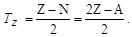
| (1.10.2) |
В соответствии с этим правилом ядра могут образовывать зарядовые мультиплеты. Ядра 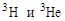 образуют зарядовый дублет:
образуют зарядовый дублет:
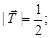 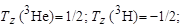 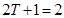 . .
|
Примером изотопического триплета является триада из рассмотренных выше пионов, для которых изоспин равен 1.
Кроме мультиплетов возможно образование зарядовых синглетов. Например, ядра 2H и 4He не имеют изобарных аналогов:
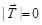 ; Тz = 0; 2Т +1 =1. ; Тz = 0; 2Т +1 =1.
|
В ядерных реакциях выполняется закон сохранения изотопического спина, что накладывает определенные ограничения на ядерные процессы. Например, a-частица (Т = 0) может испуститься ядром только в том случае, если его начальное и конечное состояния имеют одинаковый изоспин.
Изотопические соотношения проявляются особенно четко у легких ядер, так как они верны с точностью до кулоновского взаимодействия, а у ядер с небольшими Z действие электромагнитных сил проявляется слабо (см. (1.9.3)).
Статистика
Статистика – коллективное свойство системы взаимодействующих частиц, связанное с неразличимостью частиц и вероятностным характером описания состояний системы в квантовой механике. Определение этого понятия будет дано ниже. Статистика проявляется для систем, состоящих из не менее двух микрочастиц одной природы – одинаковых микрочастиц. Одинаковые микрочастицы имеют равные массы, электрический заряд, спин и другие характеристики, с помощью которых отличают микрочастицы одного сорта от микрочастиц другого сорта. Нельзя пронумеровать микрочастицы одной природы, чтобы можно было следить за движением каждой из них вдоль соответствующей траектории, уже хотя бы потому, что понятие траектории в квантовой теории теряет смысл. Поэтому вводится понятие тождественности частиц, согласно которому все одинаковые частицы, образующие данную квантовомеханическую систему, оказываются абсолютно неразличимыми. Если в системе тождественных частиц поменять местами две частицы, то перестановка частиц не приведет ни к каким изменениям в состоянии системы и не может быть экспериментально обнаружена.
Пусть имеется простейшая система из двух тождественных частиц. Состояние каждой из частиц в пространстве задается тремя координатами и проекцией спина на выбранную ось. Обозначим эти состояния каждой из частиц как ζ1 и ζ2 соответственно. Такая система описывается волновой функцией ψ(ζ1,ζ2). В силу принципа тождественности частиц, состояния системы, получающейся в результате простой перестановки обеих частиц, должно быть физически эквивалентным исходному состоянию. В квантовой механике доказывается, что
| ψ(ζ2,ζ1) = ± ψ(ζ1,ζ2). | (1.11.1) |
Таким образом, при перестановке частиц волновая функция системы либо не меняется, либо меняет свой знак. Функцию, которая не меняет свой знак при перестановке пары частиц, называют симметричной, в противном случае – ан
Дата добавления: 2021-07-22; просмотров: 809;











