Магнитный момент ядра
Магнитный момент – основная физическая величина, характеризующая магнитные свойства вещества и вызывающая ориентацию тел относительно вектора индукции внешнего магнитного поля. Магнитными моментами обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитные моменты отдельных элементарных частиц (электронов, протонов, нейтронов) обусловлены существованием у них спина (см. пояснения к (1.6.10)). Магнитные моменты ядер складываются из собственных магнитных моментов протонов и нейтронов, образующих эти ядра, а также из магнитных моментов, связанных с орбитальным движением протонов (орбитальный магнитный момент нейтрона равен нулю), по тем же правилам, по которым вычисляется спин ядра.
В соответствии с (1.6.10) магнитный момент ядра
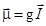 , , 
| (1.6.11) |
где g – гиромагнитное отношение, равное отношению величин магнитного и механического моментов:
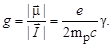 
| (1.6.12) |
В (1.6.12) приняты следующие обозначения: е– элементарный электрический заряд; mp – масса протона; с – скорость света в вакууме; γ– безразмерное число, называемое гиромагнитным множителем. Абсолютное значение вектора магнитного момента ядра
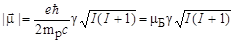 , , 
| (1.6.13) |
где I - квантовое число спина ядра. Величина
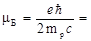 5,05×10-27 Дж/Тл 5,05×10-27 Дж/Тл
| (1.6.14) |
называется ядерным магнетоном Бора. Магнетон Бора является такой же удобной единицей измерения магнитных моментов ядер и нуклонов, какой служит элементарный электрический заряд е для измерения заряда микрочастиц, или постоянная планка 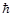 для измерения их механических моментов. Точно так же безразмерное число γ= М/μБ служит для измерения магнитных моментов ядер в единицах
для измерения их механических моментов. Точно так же безразмерное число γ= М/μБ служит для измерения магнитных моментов ядер в единицах 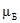 ядерного магнетона Бора, подобно тому, как атомный номер
ядерного магнетона Бора, подобно тому, как атомный номер 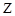 служит для измерения заряда ядер в единицах е, или квантовые числа служат для измерении механических моментов в единицах
служит для измерения заряда ядер в единицах е, или квантовые числа служат для измерении механических моментов в единицах 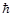 постоянной Планка. Ядерный магнетон Бора в
постоянной Планка. Ядерный магнетон Бора в 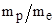 =1836 раз меньше электронного МБ магнетона Бора, который используется в атомной физике.
=1836 раз меньше электронного МБ магнетона Бора, который используется в атомной физике.
Максимальная величина проекция магнитного момента 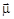 ядра на ось Z, которая совпадает с направлением внешнего по отношению к ядру магнитного поля, будет равна, согласно (1.6.4):
ядра на ось Z, которая совпадает с направлением внешнего по отношению к ядру магнитного поля, будет равна, согласно (1.6.4):
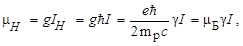
| (1.6.15) |
Методы экспериментального определения спина и магнитного момента ядер тесно между собой связаны и основаны на исследовании взаимодействия магнитного момента ядра с магнитным полем. Исторически одним из первых методов определения спина ядер было исследование сверхтонкой структуры спектральных линий атомов, возникающих в результате взаимодействия магнитного момента ядра 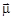 с магнитным полем
с магнитным полем 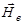 , которое создается валентными электронами атома в месте расположения ядра. Энергия взаимодействия магнитного момента ядра с магнитным полем
, которое создается валентными электронами атома в месте расположения ядра. Энергия взаимодействия магнитного момента ядра с магнитным полем 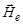 электронной оболочкой равна
электронной оболочкой равна
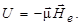
| (1.6.16) |
Вектор магнитного поля 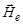 направлен противоположно вектору полного механического момента
направлен противоположно вектору полного механического момента 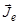 электронной оболочки атома и равен, согласно (1.6.10),
электронной оболочки атома и равен, согласно (1.6.10),
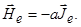
| (1.6.17) |
Константа a в (1.6.17) может быть вычислена методами квантовой электродинамики.
Таким образом, из (1.6.11), (1.6.12) и (1.6.17) получаем
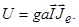
| (1.6.18) |
Полный механический момент 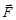 атома будет равен векторной сумме спина ядра
атома будет равен векторной сумме спина ядра 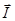 и механического момента
и механического момента 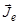 электронной оболочки:
электронной оболочки:

| (1.6.19) |
Возводим в квадрат вектор 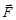 :
:
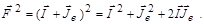
| (1.6.20) |
Из последнего соотношения находим скалярное произведение 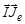 и подставляем его в (1.6.18):
и подставляем его в (1.6.18):
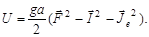
| (1.6.21) |
Выразив в (1.6.21) квадраты модулей векторов моментов через их квантовые числа, получим окончательно:
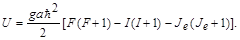
| (1.6.22) |
Таким образом, при фиксированных значениях I и Je величина энергии U взаимодействия магнитного момента ядра с магнитным полем атома определяется возможными значениями вектора 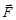 , который, согласно правилу (1.6.8) сложения моментов, может иметь (2I + 1) или (2Jе + 1) значений (берется наименьшее из чисел I или Jе). Следовательно, энергия атома для фиксированных I и Jе расщепляется на (2I + 1) или (2Jе + 1) близко расположенных подуровней (см. рис.1.6.2), что и определяет число спектральных линий сверхтонкого расщепления. Рассмотрим возможные случаи.
, который, согласно правилу (1.6.8) сложения моментов, может иметь (2I + 1) или (2Jе + 1) значений (берется наименьшее из чисел I или Jе). Следовательно, энергия атома для фиксированных I и Jе расщепляется на (2I + 1) или (2Jе + 1) близко расположенных подуровней (см. рис.1.6.2), что и определяет число спектральных линий сверхтонкого расщепления. Рассмотрим возможные случаи.
1. Jе > I. По правилу сложения моментов, квантовое число полного момента F может принимать (2I + 1) значений, которые и будут определять число линий сверхтонкого расщепления. Подсчитав это число и приравняв его числу (2I + 1) непосредственно находим спин ядра (квантовое число спина).
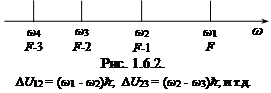 2. 1 > Jе. В этом случае, если линий сверхтонкого расщепления больше двух, применяют правило интервалов. Величина интервала ΔU12, т.е. разность значений энергии U1 и U2, которые определяются для двух соседних значений F = I + Je и F – 1 = I + Je –1 при фиксированных величинах Jе и I (см. рис.1.6.2), равна:
2. 1 > Jе. В этом случае, если линий сверхтонкого расщепления больше двух, применяют правило интервалов. Величина интервала ΔU12, т.е. разность значений энергии U1 и U2, которые определяются для двух соседних значений F = I + Je и F – 1 = I + Je –1 при фиксированных величинах Jе и I (см. рис.1.6.2), равна:
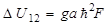 , ,
| (1.6.23) |
а величина интервала ΔU23, отвечающая двум соседним значениям F - 1 и F - 2, равна соответственно:
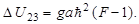
| (1.6.24) |
Отношение соседних интервалов 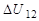 и
и 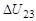
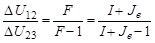 . .
| (1.6.25) |
По измеренному отношению 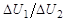 и зная Jе, определяется квантовое число I спина ядра.
и зная Jе, определяется квантовое число I спина ядра.
3. I > Jе, а линий сверхтонкой структуры всего две и правило интервалов применить нельзя (интервал всего один). Очевидно, что в этом случае Jе = 1/2 (2·1/2 + 1 = 2). Тогда вектор 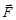 может принимать два значения: I + 1/2 и I - 1/2. Отношение интенсивностей w спектральных линий равно отношению соответствующих статистических весов (1.6.9):
может принимать два значения: I + 1/2 и I - 1/2. Отношение интенсивностей w спектральных линий равно отношению соответствующих статистических весов (1.6.9):
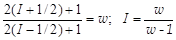 . .
| (1.6.26) |
Однако измерение отношения интенсивностей линий выполняется недостаточно точно и требуется дополнительная информация для установления спина ядра.
 Спин ядра можно также определить по расщеплению спектральных линий (эффект Зеемана) в магнитном поле, создаваемым внешним макроскопическим током, например катушкой с током.
Спин ядра можно также определить по расщеплению спектральных линий (эффект Зеемана) в магнитном поле, создаваемым внешним макроскопическим током, например катушкой с током.
Особенно точным методом определения магнитных моментов ядер является метод ядерного магнитного резонанса (ЯМР). Идея метода (И. Раби, 1939 г.) заключается в принудительном изменении ориентации магнитного момента ядра (а, следовательно, и спина), находящегося в сильном магнитном поле, под действием слабого высокочастотного магнитного поля определенной (резонансной) частоты 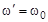 . Если образец поместить в сильное постоянное внешнее магнитное поле
. Если образец поместить в сильное постоянное внешнее магнитное поле 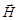 , то магнитный момент
, то магнитный момент 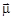 будет совершать прецессию вокруг направления
будет совершать прецессию вокруг направления 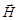 (рис.1.6.3) с частотой
(рис.1.6.3) с частотой 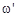 . Энергия взаимодействия магнитного момента ядра, которое находится в основном состоянии со спином I, и сильного магнитного поля равна
. Энергия взаимодействия магнитного момента ядра, которое находится в основном состоянии со спином I, и сильного магнитного поля равна
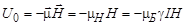 . .
| (1.6.27) |
Для перехода на следующий уровень возбуждения (изменение проекции вектора 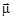 ) потребуется энергия
) потребуется энергия
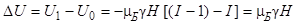 , ,
| (1.6.28) |
которой соответствует квант энергии 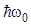 , т.е.
, т.е.
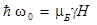 . .
| (1.6.29) |
Необходимая энергия сообщается слабым высокочастотным полем 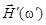 , направление которого перпендикулярно вектору
, направление которого перпендикулярно вектору 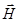 . Когда
. Когда 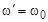 , то под действием резонансного воздействия высокочастотного поля дискретным образом изменяется положение вектора
, то под действием резонансного воздействия высокочастотного поля дискретным образом изменяется положение вектора 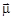 (резонансное «опрокидывание» магнитного момента из положения 0 в положение 1 на рис. 1.6.3), которое может быть замечено по максимуму поглощения высокочастотной электромагнитной энергии в этот момент. Используя полученное таким образом значение
(резонансное «опрокидывание» магнитного момента из положения 0 в положение 1 на рис. 1.6.3), которое может быть замечено по максимуму поглощения высокочастотной электромагнитной энергии в этот момент. Используя полученное таким образом значение 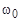 , из (1.6.29) определяется гиромагнитный множитель γ (магнитный момент в единицах
, из (1.6.29) определяется гиромагнитный множитель γ (магнитный момент в единицах 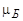 ).
).
Резонансные методы измерения магнитных моментов отличаются высокой точностью (до 6 знаков). Метод магнитного резонанса имеет несколько модификаций, в зависимости от способа обнаружения переориентации магнитных моментов в резонансном поле. Этот метод был успешно использован для измерения магнитного момента нейтрона с тем различием, что вместо образцов, содержащих ядра, использовались нейтронные пучки.
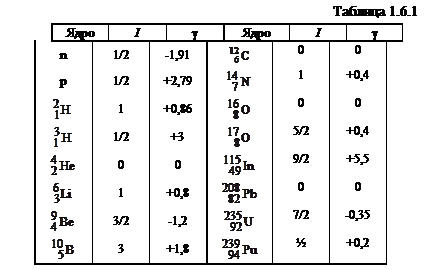 В таблице 1.6.1 приведены спины I и приближенныезначения магнитных моментов γ в единицах
В таблице 1.6.1 приведены спины I и приближенныезначения магнитных моментов γ в единицах 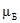 ядерного магнетона Бора для нуклонов и некоторых легких, средних и тяжелых ядер. Знак минус у величины вектора магнитного момента ядра указывает на то, что он направлен противоположно вектору спина. Ядра, имеющие нулевой спин, обладают нулевым магнитным моментом в полном соответствии с (1.6.10). Отличие магнитных моментов нуклонов от целочисленных значений, а также наличие магнитного момента у нейтрона, имеющего нулевой электрический заряд, еще не объяснено полностью. Однако эти факты с определенностью указывают на то, что нуклоны имеют внутреннюю структуру (см. §1.9 п.8).
ядерного магнетона Бора для нуклонов и некоторых легких, средних и тяжелых ядер. Знак минус у величины вектора магнитного момента ядра указывает на то, что он направлен противоположно вектору спина. Ядра, имеющие нулевой спин, обладают нулевым магнитным моментом в полном соответствии с (1.6.10). Отличие магнитных моментов нуклонов от целочисленных значений, а также наличие магнитного момента у нейтрона, имеющего нулевой электрический заряд, еще не объяснено полностью. Однако эти факты с определенностью указывают на то, что нуклоны имеют внутреннюю структуру (см. §1.9 п.8).
Дата добавления: 2021-07-22; просмотров: 554;











