Необходимость и классификация моделей
Атомное ядро представляет сложную многочастичную квантовую систему с сильным взаимодействием, обладающее чрезвычайно большим количеством свойств, порой противоречивых, и с теоретической точки зрения – объект исключительно сложный. Поэтому попытка создания последовательной и единой теории ядра сталкивается с целым рядом трудностей. При переходе от атома к ядру оказывается, что мы не располагаем достаточными знаниями о свойствах ядерных сил во всех деталях, необходимых для построения такой же законченной математической теории, как строение атома. Между частицами в атоме действуют электромагнитные силы, теория которых хорошо разработана и согласуется с экспериментом. Но предположив, что характер ядерных сил, действующих между нуклонами известен, остается проблема решения квантовой задачи многих тел, которая к настоящему времени не решена даже в случае трех тел. В этих условиях силы взаимодействия между нуклонами приходится подбирать путем подгонки к известным экспериментальным данным с помощью феноменологических постоянных и модельных зависимостей.
Из всего сказанного следует, что теория атомного ядра должна с необходимостью идти по пути создания ядерных моделей, предназначенных для описания выбранной совокупности ядерных свойств или явлений сравнительно простыми математическими способами с минимальным количеством определяемых параметров. Такой подход неизбежен уже потому, что природные объекты имеют бесконечное количество свойств и связей. Ценность любой модели определяется количеством необходимых параметров и возможностью предсказания новых свойств ядер или объяснения уже имеющихся. Но при этом, разумеется, любая модель обладает ограниченными возможностями и не может дать полного описания всех свойств ядра. В результате в ядерной физике приходится прибегать к большому числу моделей, приспособленных для описания ограниченного круга той или иной совокупности явлений, но которые вместе отвечают современному уровню наших знаний о ядре.
С теоретической точки зрения в основу любой модели кладут допущение о приближенной независимости какого-либо набора степеней свободы для выбранного объекта. Степени свободы можно классифицировать на одночастичные, отвечающие независимому движению отдельных нуклонов, и коллективные, соответствующие согласованному движению большого числа частиц.
Здесь будут рассмотрены две модели: капельная, основанная на коллективных степенях свободы, и оболочечная, использующая одночастичное описание движения нуклонов.
Капельная модель
В основу капельной модели (Вейцзеккер, 1935г., Бор, 1936г.) положено сходство в поведение атомного ядра и заряженной капли жидкости. Ядра имеет достаточно четко определенный радиус R ~ A1/3 (см. формулу (1.5.2)), из чего следует:
практически одинаковая (не зависящая отА) концентрация нуклонов в ядрах
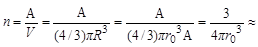 1038 см-3; 1038 см-3;
| (2.2.1) |
одинаковая плотность ядерного вещества
| ρ = mN ·n = 1,66·10-24·1038 ≈ 1014 г/см3 = 108 т/см3; | (2.2.2) |
и одинаковые средние расстояния между нуклонами:
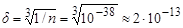 см. см.
| (2.2.3) |
Эти цифры говорят о совершенно необычном, прямо-таки потрясающем, с точки зрения макроскопических тел, состоянии ядерного вещества (например, для обычных твердых тел n » 1022см-3 , ρ » 10 г/см3, δ » 5·10-8 см).
То, что плотность ядерного вещества всех ядер постоянна, свидетельствует о его несжимаемости. Это свойство сближает ядерное вещество с жидкостью. Постоянство удельной энергии 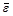 связи нуклонов в ядре углубляет аналогию. Основанием к такому предположению служит, прежде всего, тот факт, что химические силы, действующие между молекулами в жидкости, и ядерные силы, действующие между нуклонами в ядре, являются короткодействующими. Все это позволяет построить капельную модель атомного ядра, согласно которой ядро представляет сферическую каплю заряженной сверхплотной жидкости.
связи нуклонов в ядре углубляет аналогию. Основанием к такому предположению служит, прежде всего, тот факт, что химические силы, действующие между молекулами в жидкости, и ядерные силы, действующие между нуклонами в ядре, являются короткодействующими. Все это позволяет построить капельную модель атомного ядра, согласно которой ядро представляет сферическую каплю заряженной сверхплотной жидкости.
Основным результатом капельной модели является полуэмпирическая формула Вейцзеккера, в которую для получения лучшего согласия с наблюдаемыми величинами пришлось добавить члены, которые не связанны с моделью жидкой капли. Эта формула позволяет с хорошей точностью (< 1 %) вычислять энергию связи ядер по заданным значениямАи Z:
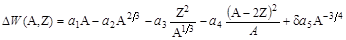 , ,
| (2.1.1) |
где a1, … a5, и d - постоянные величины. Коэффициенты, a1, … , a5 подбираются таким образом, чтобы получить наилучшее согласие со значениями энергии связи для большинства всех известных ядер. Коэффициент а3 может быть вычислен теоретически (см. ниже).
Приведемих величины:
a1 = 15,75 МэВ; a2 = 17,8 МэВ; a3 = 0,71 МэВ; a4 = 23,7 МэВ;
a5 = 34 МэВ.
Рассмотрим последовательно физический смысл всех членов формулы Вейцзеккера.
Первый член а1A в этой формуле предполагает, что все нуклоны в ядре равноценны относительно ядерного взаимодействия, и определяет примерно линейную зависимость энергии связи ΔW от А, отражая свойство насыщения ядерных сил, рассмотренное в §1.4 п.1. Однако, обращает внимание отличие вдвое коэффициента а1 от 8 МэВ – приблизительной величины энергии связи для большинства стабильных нуклидов (см. рис.1.4.2). Это вызвано учетом поправок на уменьшение энергии связи, которое учитывается последующими членами формулы Вейцзеккера.
Второй член а2A2/3 учитывает, что нуклоны, находящиеся у поверхности ядра, не испытывают насыщения всех своих возможных связей и связаны с ядром слабее, так как испытывают одностороннее притяжение вглубь ядра. Количество периферийных нуклонов определяется поверхностью ядра S ~ 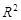 , которая, в силу (1.5.2), пропорциональна A2/3.
, которая, в силу (1.5.2), пропорциональна A2/3.
Третий член а3· 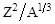 в формуле определяет, что протоны, кроме ядерного притяжения со стороны нуклонов ядра, испытывают взаимное кулоновское отталкивание, энергия которого пропорциональна Z2/R. Кулоновские силы не испытывают насыщения, и каждый из Z протонов взаимодействует со всеми остальными Z – 1; таким образом Z(Z - 1) ≈ Z2. Коэффициент а3 может быть вычислен на основании представления о равномерном распределении электрического заряда по объему сферы радиуса R:
в формуле определяет, что протоны, кроме ядерного притяжения со стороны нуклонов ядра, испытывают взаимное кулоновское отталкивание, энергия которого пропорциональна Z2/R. Кулоновские силы не испытывают насыщения, и каждый из Z протонов взаимодействует со всеми остальными Z – 1; таким образом Z(Z - 1) ≈ Z2. Коэффициент а3 может быть вычислен на основании представления о равномерном распределении электрического заряда по объему сферы радиуса R:
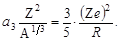
| (2.2.5) |
Это соотношение позволяет найти коэффициент  , если известна величина Rили, наоборот, подсчитать радиус ядра R по известному коэффициенту
, если известна величина Rили, наоборот, подсчитать радиус ядра R по известному коэффициенту  для всех ядер. Если в формуле (1.5.2) принять r0 = 1,3·10-13 см, то величина а3 = 0,66 МэВ.
для всех ядер. Если в формуле (1.5.2) принять r0 = 1,3·10-13 см, то величина а3 = 0,66 МэВ.
Если ограничиться только этими тремя слагаемыми, следующими из капельной модели, то оказывается, что устойчивость ядра должна возрастать с увеличением числа нейтронов в ядре при заданном числе протонов. Однако экспериментальные данные указывают на иную тенденцию. Поэтому в состав полуэмпирической формулы (2.2.4) введен четвертый член, который носит название поправки на энергию симметрии, и не следуетиз модели жидкой капли, а отражает наблюдаемую в природе тенденцию к симметрии в строении ядер. Считается установленным, что при отсутствии кулоновских сил максимум удельной энергии связи 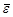 при фиксированном А соответствовал бы всем ядрам с равным числом протонов Z и нейтронов N (эффект симметрии), т.е. Z = N = A/2. Это обусловлено зарядовой независимостью ядерных сил (см. §1.10), и необходимостью выполнения принципа Паули (см. §1.11) для двух нуклонов одной природы, которые имеют спин 1/2. Равное число протонов и нейтронов у легких ядер, лежащих на дорожке стабильности (см. рис. 1.1.1 и 1.1.2), когда энергия взаимного кулоновского отталкивания протонов мала, косвенно подтверждает это положение. Для компенсации расталкивающего действия кулоновских сил, величина которых ~ Z2 (см. пояснения к третьему члену формулы), у стабильных тяжелых ядер N > Z , но кулоновская энергия уже учтена в третьем члене, и поэтому четвертый член действителен также для средних и тяжелых ядер. Отклонение от равенства Z = A/2 в любую сторону ведет к уменьшению удельной энергии
при фиксированном А соответствовал бы всем ядрам с равным числом протонов Z и нейтронов N (эффект симметрии), т.е. Z = N = A/2. Это обусловлено зарядовой независимостью ядерных сил (см. §1.10), и необходимостью выполнения принципа Паули (см. §1.11) для двух нуклонов одной природы, которые имеют спин 1/2. Равное число протонов и нейтронов у легких ядер, лежащих на дорожке стабильности (см. рис. 1.1.1 и 1.1.2), когда энергия взаимного кулоновского отталкивания протонов мала, косвенно подтверждает это положение. Для компенсации расталкивающего действия кулоновских сил, величина которых ~ Z2 (см. пояснения к третьему члену формулы), у стабильных тяжелых ядер N > Z , но кулоновская энергия уже учтена в третьем члене, и поэтому четвертый член действителен также для средних и тяжелых ядер. Отклонение от равенства Z = A/2 в любую сторону ведет к уменьшению удельной энергии 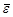 связи ядра (A,Z) и четвертый член в формуле должен быть отрицательным. Поэтомуразность (N - Z) необходимо возвести в квадрат и разделить на А (отнести к одному нуклону). Так как N = A - Z, то четвертый член приобретает вид a4·(A – 2Z)2/A.
связи ядра (A,Z) и четвертый член в формуле должен быть отрицательным. Поэтомуразность (N - Z) необходимо возвести в квадрат и разделить на А (отнести к одному нуклону). Так как N = A - Z, то четвертый член приобретает вид a4·(A – 2Z)2/A.
Последний член в формуле (2.2.4) отражает распространенность стабильных элементов и учитывает эффект спаривания одинаковых нуклонов (см. §1.4 п.3). Ядра, у которых числа N и Z - четные (Ч-Ч ядра) имеют удельную энергию связи примерно на 1 Мэв большую, чем соседние ядра, у которых либо N, либо Z - нечетные (Ч‑Н и Н-Ч ядра). Ядра с нечетным числом и протонов, и нейтронов (Н-Н ядра) имеют наименьшую удельную энергию связи среди соседних ядер. Стабильных ядер последнего типа, как отмечалось в §1.1, известно всего четыре.В соответствии с этим величина δ в пятом члене формулы Вейцзеккера принимает три значения:

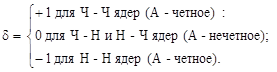
Таким образом, для четных А формула (2.2.4) двузначна.
Остановимся на некоторых следствиях из формулы Вейцзеккера. По заданным А и Z можно:
1. Вычислить массу ядра. Из формулы (1.4.11)
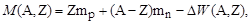
| (2.2.6) |
если энергию связи 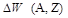 ядра рассчитать по формуле (2.2.4).
ядра рассчитать по формуле (2.2.4).
2. Найти удельную (среднюю) энергию связи 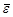 нуклона для любого нуклида.
нуклона для любого нуклида.
3. Найти среднюю энергию связи (отделения) протона и нейтрона в ядре
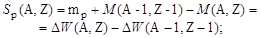
| (2.2.7) |
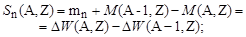
| (2.2.8) |
и любой группы связанных нуклонов, например α-частицы:
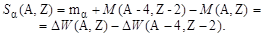
| (2.2.9) |
Если Sα < 0, то получаем энергию α-распада.
 4. Найти Z0 нуклида, устойчивого по отношению к β-распаду, для любой группы изобар. На рис. 2.2.1 представлена зависимость (2.2.6) массы ядра от Z для ядер изобаров, имеющих нечетное число нуклонов (а) и – четное число нуклонов (б). Кривые построены в соответствие с формулой (2.2.6) и их следует понимать условно, так как физический смысл имеют значения массы ядер только для дискретных значений Z. Переходы в состояния с меньшей массой показаны на рисунке стрелками. Кривая I на рис. 2.2.1 б) соответствует нестабильным относительно β-распада нечетно-нечетным ядрам. Причем некоторые из ядер могут испытывать (см. §3.5) как электронный распад, так и позитронный распад, или же Е‑захват. Изобары, лежащие на кривой II, могут иметь по несколько стабильных нуклидов, так как двойной β-распад неизвестен.
4. Найти Z0 нуклида, устойчивого по отношению к β-распаду, для любой группы изобар. На рис. 2.2.1 представлена зависимость (2.2.6) массы ядра от Z для ядер изобаров, имеющих нечетное число нуклонов (а) и – четное число нуклонов (б). Кривые построены в соответствие с формулой (2.2.6) и их следует понимать условно, так как физический смысл имеют значения массы ядер только для дискретных значений Z. Переходы в состояния с меньшей массой показаны на рисунке стрелками. Кривая I на рис. 2.2.1 б) соответствует нестабильным относительно β-распада нечетно-нечетным ядрам. Причем некоторые из ядер могут испытывать (см. §3.5) как электронный распад, так и позитронный распад, или же Е‑захват. Изобары, лежащие на кривой II, могут иметь по несколько стабильных нуклидов, так как двойной β-распад неизвестен.
На основании формулы (2.2.6) можно получить условие устойчивости ядер относительно β-распада. Очевидно, что наиболее устойчивые изобары должны иметь минимальную массу М при заданном числе А нуклонов. Для нахожденияминимума решаем уравнение
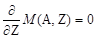
| (2.2.10) |
откуда находим
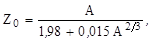
| (2.2.11) |
если в формуле (2.2.4) использовать приведенные выше значения коэффициентов а1 ÷ а5. Полученное выражение (2.2.11) является, по существу, уравнением дорожки стабильности и позволяет определять Z0 для заданных А с точностью ±1. Из (2.2.11) следует, что для β-стабильных ядер при малых значениях А (легкие ядра) Z0 ≈ 0,5A, а для тяжелых (А = 238) Z0 ≈ 0,39A, что совпадает с экспериментальными данными на рис. 1.1.2.
5. Проникновение нуклона в ядро-каплю приводит из-за малой сжимаемости ядерного вещества к коллективному движению нуклонов, вызывающих деформацию ядра без изменения его объема, в результате чего оно принимает форму эллипсоида или более сложной фигуры и возможно возникновение колебаний ядерной жидкости.
6. Капельная модель позволяет построить качественную модель деления тяжелых ядер.
Наряду с отмеченными достоинствами капельной модели, перечислим и ее некоторые основные недостатки. Капельная модель учитывает коллективное взаимодействие нуклонов между собой, но совершенно не учитывает взаимодействия и свойства отдельных нуклонов. Поэтому капельная модель приводит к плавной зависимости свойств ядер от числа и состава нуклонов в ядре. Ряд свойств ядра – удельная энергия связи ядра 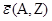 , спин ядра, магнитный и электрический моменты изменяются периодически от числа нуклонов в ядре. Четно-четные ядра в основном состоянии имеют нулевые значения спина, магнитнного и электрического дипольного моментов. Капельная модель не объясняет наличия магических чисел, не дает правильного описания возбужденных уровней легких и средних ядер, не объясняет асимметрию деления ядер, хотя и используется довольно плодотворно в теории деления ядер.
, спин ядра, магнитный и электрический моменты изменяются периодически от числа нуклонов в ядре. Четно-четные ядра в основном состоянии имеют нулевые значения спина, магнитнного и электрического дипольного моментов. Капельная модель не объясняет наличия магических чисел, не дает правильного описания возбужденных уровней легких и средних ядер, не объясняет асимметрию деления ядер, хотя и используется довольно плодотворно в теории деления ядер.
Оболочечная модель
Ядра, содержащие магическое число нейтронов или протонов, т.е. 2, 8, 20, 50, 82, 126 (только для нейтронов), обладают повышенной удельной энергией связи по сравнению с «соседними» ядрами, имеют большую распространенность в природе. Нуклиды с магическими ядрами имеют наибольшее число стабильных изотопов и изотонов. Ядра с магическими числами N поглощают нейтроны с вероятностью, меньшей в 10 ÷ 100 раз, чем ядра с близкими значениями N. Периодичность изменения этих и ряда других свойств ядер при изменении A и Z напоминает периодическое изменение свойств атомов от числа содержащихся в них электронов. Это наводит на мысль о наличии в ядрах устойчивых заполненных оболочек подобно тому, как это имеет место в атомах, где магическими являются числа 2, 10, 18, 36, 54, 86 для электронов в заполненных оболочках инертных газов. В обоих случаях физической причиной периодичности является принцип Паули (см. §1.11).
Современная модель атома строится в предположении о независимом (от других электронов) движении электрона в центральном электрическом поле ядра. Поэтому можно предположить, что периодичность в свойствах ядер удастся объяснить в модели независимых частиц. Но ядро состоит из сильно взаимодействующим между собой нуклонов и не имеет явно выраженного источника поля центральных сил. Поэтому, в отличие от модели атома, сама идея модели независимых частиц на первый взгляд представляется спорной.
Основные предположения при построении оболочечной модели следующие.
1. Нуклоны двигаются в сферически симметричном самосогласованном поле ядерных сил, создаваемом всеми нуклонами ядра, т.е. реальные силы, действующие между нуклонами, заменяются действием общего для всех нуклонов силового центра. Из-за тесного со 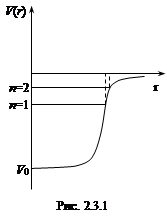 седства нуклонов (расстояние между центрами нуклонов (2.2.3) δ ≈ 2·10‑13 см) и малого радиуса действия ядерных сил средний потенциал должен быть близок к однородному внутри ядра и быстро изменяться на границе ядра (рис. 2.3.1). При этом необходимо учесть спин-орбитальное взаимодействие, которое выражается в том, что нуклон испытывает более интенсивное притяжение полем ядерных сил тогда, когда векторы спина и орбитального момента нуклона направлены в одну сторону. Поэтому гамильтониан взаимодействия Н(r) может быть представлен в виде
седства нуклонов (расстояние между центрами нуклонов (2.2.3) δ ≈ 2·10‑13 см) и малого радиуса действия ядерных сил средний потенциал должен быть близок к однородному внутри ядра и быстро изменяться на границе ядра (рис. 2.3.1). При этом необходимо учесть спин-орбитальное взаимодействие, которое выражается в том, что нуклон испытывает более интенсивное притяжение полем ядерных сил тогда, когда векторы спина и орбитального момента нуклона направлены в одну сторону. Поэтому гамильтониан взаимодействия Н(r) может быть представлен в виде
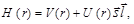
| (2.3.1) |
а V(r) – так называемый потенциал Вудса-Саксона (рис. 2.3.1), совпадающий по форме с распределением (1.5.3) плотности ядерного вещества в ядре:
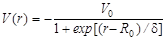 , ,
| (2.3.2) |
а U(r) – центрально-симметричный потенциал, более слабый, чем V(r). Обычно полагают, что
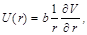
| (2.3.3) |
где b – константа спин-орбитального взаимодействия. Последний член в (2.3.1) учитывает знак и величину спин-орбитального взаимодействия посредством скалярного произведения вектора  спина нуклона и вектора
спина нуклона и вектора  его орбитального момента.
его орбитального момента.
2. Нуклоны, двигаясь в потенциальной яме, могут находиться только на различных дискретных энергетических уровнях. Основному состоянию ядра соответствует полное заполнение самых нижних уровней. При движении нуклоны могут сталкиваться и обмениваться энергией, в результате чего энергия одного из нуклонов может уменьшиться и тогда он должен оказаться на одном из более низких энергетических уровней. Но эти уровни уже заполнены и на них, согласно принципу Паули, добавочные нуклоны находиться не могут. Этим оправдывается предположение об отсутствии взаимодействия между нуклонамии, как следствие, возможность одночастичной характеристики их состояний с помощью набора квантовых чисел.
Состояние нуклона (одночастичное состояние) в потенциальной яме (2.3.1) характеризуется квантовыми числами n, l, j, mj и определенной четностью.
Число n = 1, 2, 3, . . . – главное квантовое число нумерует энергетические уровни нуклона. Чем больше энергия нуклона, тем больше n и тем больше среднее расстояние нуклона от центра ядра (см. рис. 2.3.1).
Уровни с квантовыми числами орбитального момента l = 0, 1, 2, и т.д. (орбитальный момент может иметь только целочисленные значения (см. §1.6 п.1)) обозначаются соответственно буквами s (не путать с обозначением спина), p, d, f и далее по алфавиту. По правилу сложения квантовомеханических векторов (1.6.8) для l > 0 квантовое число j полного момента может иметь только два значения
| j = l ± 1/2, | (2.3.5) |
а для l = 0 имеет одно значение.Таким образом, в результате спин-орбитального взаимодействия каждый уровень с заданными n и l > 0 расщепляется на два подуровня с различными значениями энергии, которые всегда выражаются положительными полуцелыми числами: 1/2, 3/2, 5/2, и т.д. Более высокому подуровню соответствует j = l - 1/2. Величина расщепления определяется величиной l, и поэтомуоно особенно велико для больших орбитальных моментов.
Через mj обозначается проекция полного момента нуклона (азимутальное квантовое число), которая имеет 2j + 1 значений: mj = -jћ, -(j+1)ћ, . . . , (j-1)ћ, jћ.
Каждый из уровней обладает определенной четностью (-1)l (см. (1.8.10)), которая определяется четностью квантового числа l.
Обозначение уровней нуклона в ядре или систематика уровней имеет следующий вид. Первой ставится цифра главного квантового числа n, затем следует буква, обозначающая квантовое число орбитального момента l (s, p, d, . . .), нижний правый индекс которой равен квантовому числу j полного момента нуклона. Например, через 1р3/2 обозначается уровень с n = 1, l = 1 и j = 3/2. Квантовое числопроекции полного момента j на ось обычно не указывается, так как для сферически симметричного потенциала уровни, различающиеся по j, имеют одинаковые энергии.
Для получения системы одночастичных уровней нейтронов конкретного ядра (A,Z) задают константы в (2.3.2) и (2.3.3) и решают уравнение Шредингера. При переходе от ядра к ядру эти константы приходится подбирать вновь. Оказалось, что, подбирая значения констант, можно получить группы тесно расположенных уровней, которые принято называть оболочкой. Оболочки, в свою очередь, разделены относительно большими энергетическими промежутками (рис. 2.3.2).

|
Для получения системы уровней протонов в (2.3.1) необходимо ввести самосогласованный сферически-симметричный потенциал электрического поля, описывающий взаимодействие с ядром отдельного протона. Поэтому схема уровней для протонов будет отличаться от нейтронной главным образом величиной энергии для заданных n и l, а общая схема заполнения уровней протонных оболочек остается примерно той же самой.
С помощью модели оболочек удается получить заполнение более высоких оболочек и все значения магических чисел: 2, 8, 20, 50, 82, 126.
Из модели оболочек следует, что:
1. Основные состояния дважды магических ядер должны иметь характеристику 0+, т.е. каждая заполненная оболочка имеет нулевой спин и положительную четность.
2. Характеристика основного состояния ядра, имеющего на один нуклон больше дважды магического, определяется характеристикой уровня, следующего поверх оболочки магического числа. Например, спин ядра 17О должен определяться одним девятым нейтроном на нижнем уровне третьей оболочки (см. рис. 2.3.2) сверх заполненной второй, который, очевидно, будет находиться на уровне 1d5/2, то есть иметь характеристику 5/2+, что подтверждается опытом.
3. Характеристика основного состояния ядра, имеющего на один нуклон меньше дважды магического ядра, определяется характеристикой высшего уровня оболочки, соответствующей магическому числу, на которой должен находиться недостающий нуклон. Например, в ядре 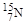 не хватает одного протона до дважды магического ядра
не хватает одного протона до дважды магического ядра 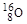 . Вторая протонная оболочка для магического числа Z = 8 заканчивается высшим уровнем 1р1/2 (см. рис. 2.3.2). Поэтому основное состояние ядра
. Вторая протонная оболочка для магического числа Z = 8 заканчивается высшим уровнем 1р1/2 (см. рис. 2.3.2). Поэтому основное состояние ядра 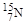 должно, и действительно имеет характеристику 1/2-. Во всех случаях четность состояний определялась как (‑1)l. Эти три правила выполняются без исключений.
должно, и действительно имеет характеристику 1/2-. Во всех случаях четность состояний определялась как (‑1)l. Эти три правила выполняются без исключений.
Оболочечная модель дает правильные границы для изомерных[2]ядер в процессе заполнения IV и V оболочек.
Однако для двух и более нуклонов сверх дважды магических чисел приведенные правила не дают правильных результатов при сложении квантовомеханических векторов состояний этих нуклонов по обычным правилам. Расхождения объясняются взаимодействием этих нуклонов между собой, которое не учитывается в одночастичной модели оболочек. Простейший способ учесть взаимодействия между одноименными нуклонами – использовать эффект спаривания нуклонов, с которым мы уже неоднократно встречались (см. §1.4 п.3, §1.6 1.п.б). Модель оболочек, учитывающая эффект спаривания одноименных нуклонов, называется моделью оболочек с феноменологическим спариванием.
В этой модели предполагается, что при четном числе нуклонов одного сорта они объединяются в пары с нулевым спином, либо при нечетном числе нуклонов в пары объединяются все, за исключением одного, состояние которого должно определять спин и четность ядра. Отсюда следует:
1.Основные состояния всех четно-четных ядер имеют характеристику 0+. Это правило не имеет исключений.
2. Характеристика основного состояния ядра с нечетным А должны совпадать с характеристикой уровня, на котором располагается последний неспаренный нуклон. Например, ядро 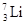 имеет два спаренных протона относительно магического числа 2 и один неспаренный протон, находящийся в состоянии 1р3/2. Соответственно основное состояние этого ядра имеет характеристику 3/2-. Это правило выполняется почти во всех случаях, за исключением ядер
имеет два спаренных протона относительно магического числа 2 и один неспаренный протон, находящийся в состоянии 1р3/2. Соответственно основное состояние этого ядра имеет характеристику 3/2-. Это правило выполняется почти во всех случаях, за исключением ядер 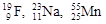 .
.
Спин и четность нечетно-нечетного ядра в такой модели должен определяться двумя неспаренными разноименными нуклонами. Поэтому спин и четность таких ядер не могут быть однозначно представлены в рассматриваемой модели. Например, если спин ядра 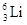 определяется моментами третьего протона и третьего нейтрона, то он должен быть равен 3, так как согласно модели оболочек оба этих нуклона должны находиться в состоянии 1р3/2. Между тем эксперимент дает спин, равный единице. Правильное значение спина дает эффект симметрии (см. §2.2), который уже не следует из модели оболочек.
определяется моментами третьего протона и третьего нейтрона, то он должен быть равен 3, так как согласно модели оболочек оба этих нуклона должны находиться в состоянии 1р3/2. Между тем эксперимент дает спин, равный единице. Правильное значение спина дает эффект симметрии (см. §2.2), который уже не следует из модели оболочек.
Оболочечная модель, несмотря на ее отмеченные успехи, имеет весьма ограниченную область применения. Она позволяет объяснить некоторые свойства сферических ядер в основном и слабо возбужденном состоянии. Она дает резко заниженные значения квадрупольных электрических моментов для ядер, число протонов в составе которых соответствует заполнению середины оболочки. Расхождения расчетных и экспериментальных величин для тяжелых ядер могут достигать 10 ÷ 20 раз. Считается, что недостатки оболочечной модели вызваны предположениями о сферичности ядерного потенциала и отсутствием учета взаимодействия между нуклонами.
Эти два фактора учитывает модель атомного ядра, которая называется обобщенной моделью ядра. В этой модели одновременно учитываются коллективные и одночастичные степени свободы, т.е. она является синтезом. Ядро предполагается состоящим из сферически симметричного остова, для описания которого используется коллективная модель. Но остов может иметь коллективные степени свободы, то есть колебаться или вращаться в целом, если принимает несферическую форму. Нуклоны вне остова могут быть описаны на основе модели независимых частиц или частиц с взаимодействием. Такая усложненная модель значительно лучше описывает возбужденные состояния ядер, их квадрупольные электрические моменты и некоторые другие характеристики.
Дата добавления: 2021-07-22; просмотров: 654;











