Основные законы радиоактивного распада
Радиоактивный распад – явление принципиально случайное. Нельзя предсказать, когда именно распадется данное радиоактивное ядро, а можно лишь указать с какой вероятностью оно распадется за тот или иной промежуток времени. Распад отдельного радиоактивного ядра не зависит от присутствия других ядер и может произойти в любой интервал времени. Наблюдения за очень большим числом одинаковых радиоактивных превращений ядер позволяет установить вполне определенные количественные закономерности для характеристики процесса радиоактивного распада.
Естественная статистическая величина, характеризующая радиоактивный распад, – постоянная (или константа) распада λ – определяет вероятность распада ядра в единицу времени и имеет размерность [время]‑1. Экспериментальные и теоретические исследования позволяют заключить, что постоянная распада λ не зависит, по-видимому, от времени, прошедшего с момента образования радиоактивного ядра, что отражено в названии.
Пусть радиоактивное ядро достоверно существует в некоторый момент времени t = 0, условно принимаемый за ноль. У такого ядра к произвольно выбранному моменту времени t может реализоваться одна из двух возможностей:
1) ядро испытало радиоактивный распад и вероятность такого события равна 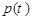 ;
;
2) ядро не испытало радиоактивного распада и вероятность такого события равна  .
.
Очевидно, что
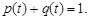
| (3.2.1) |
Установим, чему равна вероятность 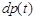 испытать ядру радиоактивный распад за интервал времени от t до (t+dt), т.е. предварительно не испытав распада за время
испытать ядру радиоактивный распад за интервал времени от t до (t+dt), т.е. предварительно не испытав распада за время 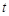 . Вероятность такого сложного события
. Вероятность такого сложного события
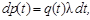
| (3.2.2) |
где λdt - вероятность распада ядра внутри временного интервала dt (постоянная распада λ не зависит от времени!). Используя (3.2.1) уравнение (3.2.2) приведем к виду
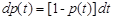 . .
| (3.2.3) |
Поскольку ядро достоверно существует в момент времени 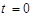 , то имеем очевидное начальное условие
, то имеем очевидное начальное условие 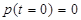 . Тогда искомая вероятность составит
. Тогда искомая вероятность составит
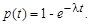
| (3.2.4) |
При помощи (3.2.1) и (3.2.4) найдем для ядра вероятность q(t) не испытать распада к моменту времени t:
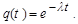
| (3.2.5) |
Соотношения (3.2.4) и (3.2.5) содержат полное описание статистических свойств радиоактивного распада ядер и позволяют определить любые статистические характеристики распада.
Найдем среднее время 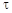 жизни ядра, используя определение для математического среднего:
жизни ядра, используя определение для математического среднего:
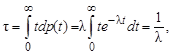
| (3.2.6) |
поскольку 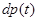 – вероятность того, что ядро, прожив время t, распадется за время между
– вероятность того, что ядро, прожив время t, распадется за время между 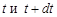 .
.
Пусть в момент времени t = 0 имелось N0 радиоактивных ядер одной природы. Наиболее вероятное (ожидаемое) число ядер N(t), которые не испытают радиоактивного распада к моменту времени t, должно составить
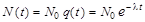 , ,
| (3.2.7) |
а соответственно число распавшихся ядер (d – decay – распад)
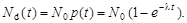
| (3.2.8) |
Формула (3.2.7) выражает основной закон радиоактивного распада. Следует еще раз подчеркнуть, что 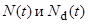 имеют смысл наиболее вероятного количества оставшихся и распавшихся радиоактивных ядер к моменту времени t. Реальные же количества радиоактивных ядер к моменту времени t могут быть как больше
имеют смысл наиболее вероятного количества оставшихся и распавшихся радиоактивных ядер к моменту времени t. Реальные же количества радиоактивных ядер к моменту времени t могут быть как больше 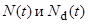 , так и меньше. Используемая далее в выражениях величина N, если не оговорено иное, всегда имеет смысл среднего числа ядер.
, так и меньше. Используемая далее в выражениях величина N, если не оговорено иное, всегда имеет смысл среднего числа ядер.
В ядерной физике и ее приложениях используется еще одна временная характеристика распада – период полураспада Т1/2, которая определяет время, за которое первоначальное количество ядер N0 должно уменьшиться в два раза. Установим связь между периодом полураспада Т1/2 и постоянной распада λ. По определению
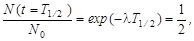
| (3.2.9) |
откуда
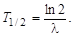
| (3.2.10) |
Сравнивая это выражение с (3.2.6) устанавливаем, что
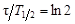
| (3.2.11) |
Для характеристики радиоактивных свойств вещества, т.е. совокупности большого числа радиоактивных ядер, служит специальная величина, характеризующая скорость радиоактивных превращений, которая называется активностью. Активность А (не путать с массовым числом А!) – среднее число ядер в образце, испытавших радиоактивный распад за единицу времени. Для радиоактивных ядер одной природы получим, используя (3.2.8):
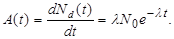
| (3.2.11) |
Полученное выражение можно записать в следующем виде (учитывая (3.2.7)):
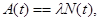
| (3.2.12) |
или же в виде
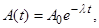
| (3.2.13) |
где 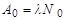 - начальная активность образца.
- начальная активность образца.
Единицей измерения активности в СИ служит беккерель (Бк),
| 1 Бк = 1 распад/с. |
Часто в практических приложениях используется другая единица измерения активности - кюри (Ки):
| 1 Ки = 3,7·1010 Бк. |
Активность, отнесенная к массе радиоактивного препарата, называется массовой удельной активностью. Для жидких и газообразных веществ иногда используют объемную удельную активность.
Для характеристики радиоактивных свойств нуклида одной природы (без учета вторичных компонент, возникающих после распада) используют удельную активность нуклида – активность единицы массы этого нуклида:
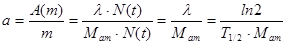 , ,
| (3.2.14) |
т.е. удельная активность нуклида не зависит от времени.
Для определения l (а, следовательно, t и Т1/2) можно использовать формулу (3.2.12), если в некоторый произвольный момент времени измерить активность препарата и число радиоактивных ядер. Этим методом удобно пользоваться, когда период полураспада достаточно велик, и поэтому изменением числа радиоактивных ядер за время измерения активности можно пренебречь. Если период полураспада Т1/2 не очень велик, то можно непосредственно снять кривую изменения активности через определенные интервалы времени. Затем по полученным значениям строят график зависимости натурального логарифма активности от времени. Постоянную распада l удобно находить, если записать (3.2.13) в виде:
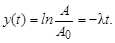
| (3.2.15) |
 Зависимость (3.2.15) представляет собой прямую, а l определяется по тангенсу угла наклона этой прямой (рис. 3.2.1) или непосредственно по уменьшению активности вдвое. В реальных условиях экспериментальные точки имеют неизбежный разброс, определяемый статистической природой процесса радиоактивного распада. Для проведения через такие точки наиболее достоверной прямой обычно используют метод наименьших квадратов, в результате чего среднеквадратичное отклонение точек от найденной прямой будет минимальным.
Зависимость (3.2.15) представляет собой прямую, а l определяется по тангенсу угла наклона этой прямой (рис. 3.2.1) или непосредственно по уменьшению активности вдвое. В реальных условиях экспериментальные точки имеют неизбежный разброс, определяемый статистической природой процесса радиоактивного распада. Для проведения через такие точки наиболее достоверной прямой обычно используют метод наименьших квадратов, в результате чего среднеквадратичное отклонение точек от найденной прямой будет минимальным.
Весьма распространенными являются случаи распада радиоактивных ядер с образованием не только стабильных, но и радиоактивных дочерних ядер. В последнем случае возникают цепочки распадов. Примером таких цепочек могут служить рассмотренные выше радиоактивные семейства. Баланс числа радиоактивных ядер при этом определяется следующими уравнениями:
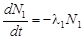
| (3.2.16) |
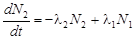
| |
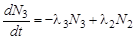
| |
| . . . . . . . . . . . . . |
где индекс 1 относится к первичным материнским ядрам, а индексы 2, 3, . . . – к дочерним. Распад ядер N1 описывается обычным законом распада (3.2.7). Баланс ядер каждого дочернего вещества определяется скоростью собственного распада (активностью) и скоростью рождения, равной скорости распада ядер-предшественников. Решение каждого уравнения (3.2.16) зависит только от вида решения предшествующего. В простейшем случае, когда в начальный момент времени дочерних ядер нет, а количество материнских ядер равно N10, решение каждого k-го уравнения из (3.2.16) имеет вид:
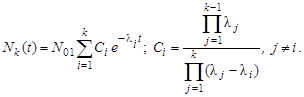
| (3.2.17) |
Полное число радиоактивных ядер есть сумма всех количеств ядер Nk, существующих в данный момент времени.
Из общего решения (3.2.17) получаем решение для N2(t):
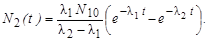
| (3.2.18) |
Из (3.2.18) следует, что в момент времени
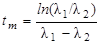 , ,
| (3.2.19) |
количество ядер N2 достигает своей максимальной величины
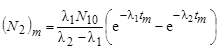 , ,
| (3.2.20) |
а затем монотонно убывает. Если l1 << l2 (или (Т1/2 )1 >> (Т1/2 )2) и t » (Т1/2 )2, то из (3.2.18) в пределе t → ∞ получаем
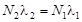 , ,
| (3.2.21) |
т.е. устанавливается динамическое равновесие между активностью материнского и дочернего препаратов, которое называется вековым равновесием. Вековое равновесие широко используется для определения периодов полураспада долгоживущих материнских нуклидов по известным значениям l2 и отношению N2/ N1. Очевидно, что при выполнении соответствующих условий вековое равновесие может наступать для любой пары соседних элементов в цепочке распадов.
Другой предельный случай l1 >> l2 (или (Т1/2 )1 << (Т1/2 )2) при t » (Т1/2 )1 дает зависимость
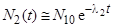 , ,
| (3.2.22) |
которая фактически является кривой распада дочернего вещества.
Активация
Активация – процесс получение из стабильных ядер радиоактивных ядер - представляет ядерную реакцию, рассмотрению которых посвящена глава 4. Выше было указано, что по физической природе искусственные радиоактивные ядра ничем не отличаются от естественных, так как свойства ядер данного радиоактивного нуклида не зависят от способа его образования. Рассмотрим основные закономерности процесса активации.
Пусть q(t) – скорость образования новых радиоактивных ядер, или количество радиоактивных ядер, образующихся в единицу времени. Тогда скорость изменения числа образующихся радиоактивных ядер за время dt составит
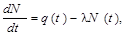
| (3.3.1) |
где 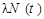 - скорость распада (активность) образующихся ядер. Если принять, что скорость образования q(t) = q – постоянна и не зависит от времени, то решение (3.3.1) с начальным условием N(t = 0) = 0 имеет вид:
- скорость распада (активность) образующихся ядер. Если принять, что скорость образования q(t) = q – постоянна и не зависит от времени, то решение (3.3.1) с начальным условием N(t = 0) = 0 имеет вид:
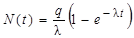 . .
| (3.3.2) |
Умножив (3.3.2) слева и справа на постоянную распада λ получим, учитывая (3.2.12), наведенную активность вещества:
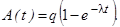
| (3.3.2) |
 На рис. 3.3.1 показана эта функция, построенная в относительных единицах. Из рисунка видно, что уже при t = 4Т1/2 наведенная активность составляет около 95 % от предельного значения.
На рис. 3.3.1 показана эта функция, построенная в относительных единицах. Из рисунка видно, что уже при t = 4Т1/2 наведенная активность составляет около 95 % от предельного значения.
Предельная или максимально достижимая активность получаемого вещества при t → ∞ не зависит, как следует из (3.3.2), от постоянной распада λ, а равняется скорости q образования радиоактивных ядер. Однако время достижения предельной активности зависит от величины λ и при уменьшении величины λ требуется большее время достижения активности насыщения и наоборот. После прекращения активации происходит только процесс распада образовавшегося вещества в соответствии с (3.2.7) или (3.2.13).
В ядерном реакторе под действием нейтронов происходит активация корпуса реактора, деталей конструкции, а также теплоноситель. Вода активируется слабо и заметный вклад в активность водного теплоносителя дает активация продуктов коррозии трубопроводов. В реакторах на быстрых нейтронах сильной активации подвергается натрий, который используется в качестве теплоносителя. Эта наведенная активность, наряду с радиоактивностью продуктов деления, является серьезным фактором, влияющим на экологические и экономические показатели АЭС.
Альфа – распад
Альфа-распадом (a-распадом) называется процесс спонтанного изменения ядра, в результате которого возникает свободная a-частица (ядро нуклида 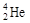 ) и дочернее ядро, имеющее в своем составе меньше на 4 нуклона и 2 протона, чем материнское. Символическая запись a-распада имеет вид:
) и дочернее ядро, имеющее в своем составе меньше на 4 нуклона и 2 протона, чем материнское. Символическая запись a-распада имеет вид:
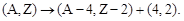
| (3.4.1) |
a-Распад характерен для тяжелых нуклидов, у ядер которых с ростом массового числа А наблюдается уменьшение удельной энергии связи (см. рис. 1.4.2). В этой области уменьшение числа нуклонов в ядре ведет к увеличению удельной энергии связи. Но при уменьшении массового числа на единицу увеличение энергии связи оказывается существенно меньше энергии связи нуклона в ядре и испускание протона или нейтрона невозможно. Однако, испускание α-частицы оказывается энергетически выгодным, так как удельная энергия связи нуклона в ядре 4Не около 7,1 МэВ и сравнима с удельной энергией связи нуклонов для тяжелых ядер. Поэтому α-распад наблюдается у ядер, тяжелее свинца (см. в §3.1 о радиоактивных семействах). Небольшое количество a-активных ядер средней массы имеется среди лантаноидов. Объясняется это тем, что количество нейтронов у нуклидов 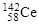 ,
, 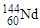 и
и 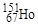 равно 84, т.е. на две единицы превышает магическое число 82, которое соответствует заполнению нейтронной оболочки. После α-распада этих ядер образуются дочерние ядра с магическим числом нейтронов, равным 82.
равно 84, т.е. на две единицы превышает магическое число 82, которое соответствует заполнению нейтронной оболочки. После α-распада этих ядер образуются дочерние ядра с магическим числом нейтронов, равным 82.
Так как при α-распаде высвобождается внутренняя энергия, то энергетическая возможность a-распада обеспечивается тогда, когда масса исходного ядра больше суммы масс ядер продуктов распада:
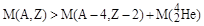 , ,
| (3.4.2) |
или, если использовать массы нейтральных атомов, как это обычно принято в ядерной физике,
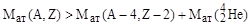 . .
| (3.4.3) |
Уменьшение массы при распаде, выраженное в энергетических единицах, дает энергию, высвобождаемую при a-распаде:
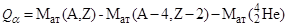 . .
| (3.4.4) |
Таким образом, a-распад становится возможным, если:
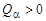 или или 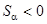 , ,
| (3.4.5) |
где 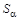 – энергия связи (отделения) α-частицы относительно материнского ядра (см. (1.4.19)). Однако условие (3.4.5) не является достаточным условием для a-распада.
– энергия связи (отделения) α-частицы относительно материнского ядра (см. (1.4.19)). Однако условие (3.4.5) не является достаточным условием для a-распада.
Выполнение условия (3.4.5) для a-распада можно теоретически оценить с помощью формулы (2.2.9), используя формулу Вайцзеккера (2.2.1). Расчет приводит к выводу о том, что Sα < 0 для Z > 73.
Энергия Ea, высвобождаемая при a-распаде, переходит в кинетическую энергию Тa движения a-частицы и кинетическую энергию ТЯ дочернего ядра. Часть энергии может также переходить в энергию Εвозб возбуждения дочернего ядра. Таким образом, если ядро, испытывающие α-распад, неподвижно в лабораторной системе координат (его импульс равен нулю), то
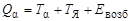 . .
| (3.4.6) |
Тогда из закона сохранения импульса следует, что абсолютные величины импульсов a-частицы (Рa ) и дочернего ядра (РЯ) равны друг другу:
| Рa = РЯ, | (3.4.7) |
Поскольку Тα << Mα и ТЯ << MЯ, то скорости a-частицы и дочернего ядра много меньше скорости света и можно воспользоваться нерелятивистской связью между импульсами и кинетической энергией:
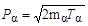 и и 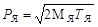 . .
| (3.4.8) |
Из последних трех соотношений получаем
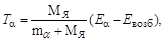
| (3.4.9) |
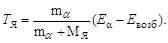
| (3.4.10) |
Из (3.4.9) и (3.4.10) получаем, что для ядер с массовым числом A > 200 Тa/ТЯ = MЯ/ma, т.е. не менее 98% кинетической энергии передается a-частице. Необходимо обратить внимание на то, что из (3.4.9) следует, что α-частицы должны иметь дискретное значение кинетической энергии.
В 1911 г. Г. Гейгер эмпирически установил, что в области пробегов α-частиц 2,5 ÷ 6 см зависимость между средней длиной пробега Rα в воздухе для α-частиц и их кинетической энергией Тα может быть представлена в виде
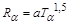 , ,
| (3.4.11) |
что позволило измерять кинетическую энергию α-частиц по длине пробега.
Особо точно измерять кинетическую энергию α-частиц оказалось возможным с помощью магнитного α-спектрометра, принцип действия которого аналогичен масс-спектрометру (рис. 1.3.1). Согласно формуле (1.3.8), радиус R окружности, по которой движется заряженная частица в однородном магнитном поле с индукцией В, прямо пропорционален ее импульсу. Если масса и заряд всех частиц одинакова, как в случае a-частиц, то выполняется анализ скоростей или кинетических энергий a-частиц.
Измерения показали, что кинетическая энергия Ta a-частиц при распаде ядер различных нуклидов меняется в пределах 4 - 9 МэВ.
 Вместе с тем при измерении энергии α-частиц с помощью α-спектрометра было установлено, что кроме основной энергетической группы, имеющей наибольшую интенсивность, часто наблюдаются группы α-частиц с меньшими энергиями. α-Частицы с меньшей, чем у основной группы, энергией имеют меньший пробег в воздухе и были названы короткопробежными α‑частицами. Энергетический спектр α-частиц изображен на рис. 3.4.1 и называется линейчатым. Высота каждой линии определяется относительным выходом η для каждой энергетической группы a-частиц. Относительные выходы короткопробежных α-частиц обычно существенно ниже, так как прозрачность (см. ниже) кулоновского барьера меньше для a-распадов с меньшим значением Тα.
Вместе с тем при измерении энергии α-частиц с помощью α-спектрометра было установлено, что кроме основной энергетической группы, имеющей наибольшую интенсивность, часто наблюдаются группы α-частиц с меньшими энергиями. α-Частицы с меньшей, чем у основной группы, энергией имеют меньший пробег в воздухе и были названы короткопробежными α‑частицами. Энергетический спектр α-частиц изображен на рис. 3.4.1 и называется линейчатым. Высота каждой линии определяется относительным выходом η для каждой энергетической группы a-частиц. Относительные выходы короткопробежных α-частиц обычно существенно ниже, так как прозрачность (см. ниже) кулоновского барьера меньше для a-распадов с меньшим значением Тα.
Испускание короткопробежных частиц всегда сопровождается γ-излучением соответствующей энергии, что свидетельствует о возбуждении дочернего ядра. Поскольку процесс a-распада носит ста  тистический характер, то ядра одной и той же природы могут возникать в различных возбужденных состояниях. Таким образом, в данном a-активном источнике, который содержит огромное количество одинаковых ядер, при α-распаде может возникать вполне закономерный набор дискретных значений энергий α-частиц и возбужденных дочерних ядер. Это поясняет диаграмма на рис. 3.4.2, где показана схема a-распада ядра 235U. Энергия каждого состояния ядра откладывается по условной оси, направленной вверх, и отмечается соответствующей горизонтальной линией, называемой уровнем. Возле каждого уровня при необходимости могут указываться энергия, спин и четность. Условная горизонтальная ось представляет изменение Z ядра. α-Переходы показаны стрелками, идущими сверху вниз налево, и указывают, что энергия и порядковый номер дочернего нуклида становятся меньше материнского, и происходит смещение влево по строке таблицы Менделеева (уменьшается Z). Слева от уровней возбужденного дочернего ядра (в данном случае это ядро 231Th) указаны энергии возбуждения в МэВ, а вертикальными стрелками – γ-переходы. Энергия каждой группы α-частиц определяется с помощью формулы (3.4.9), в которой используется энергия Евозб, соответствующая данному возбужденному уровню дочернего ядра 231Th.
тистический характер, то ядра одной и той же природы могут возникать в различных возбужденных состояниях. Таким образом, в данном a-активном источнике, который содержит огромное количество одинаковых ядер, при α-распаде может возникать вполне закономерный набор дискретных значений энергий α-частиц и возбужденных дочерних ядер. Это поясняет диаграмма на рис. 3.4.2, где показана схема a-распада ядра 235U. Энергия каждого состояния ядра откладывается по условной оси, направленной вверх, и отмечается соответствующей горизонтальной линией, называемой уровнем. Возле каждого уровня при необходимости могут указываться энергия, спин и четность. Условная горизонтальная ось представляет изменение Z ядра. α-Переходы показаны стрелками, идущими сверху вниз налево, и указывают, что энергия и порядковый номер дочернего нуклида становятся меньше материнского, и происходит смещение влево по строке таблицы Менделеева (уменьшается Z). Слева от уровней возбужденного дочернего ядра (в данном случае это ядро 231Th) указаны энергии возбуждения в МэВ, а вертикальными стрелками – γ-переходы. Энергия каждой группы α-частиц определяется с помощью формулы (3.4.9), в которой используется энергия Евозб, соответствующая данному возбужденному уровню дочернего ядра 231Th.
В некоторых случаях возникающее в результате предшествующего b-распада a-активное ядро может оказаться в возбужденном состоянии. Если периоды полураспада таких ядер относительно α-распада составляют 10-7 ÷ 10-5 с, то небольшая часть возбужденных ядер может испытать a‑распад прежде, чем перейдет в основное состояние с испусканием γ‑кванта. При этом к энергии a‑распада (3.4.4) добавляется энергия возбуждения материнского ядра, и появляются a-частицы с кинетической энергией большей, чем для a-частиц из основного состояния. Такие a-частицы носят название длиннопробежных (см. рис.3.4.1). Примерами являются нуклиды 212Ро и 214Ро, у которых периоды полураспада по отношению испускания α-частиц из основных состояний равны соответственно 3·10-7 и 2·10-4 с.
Исследование энергетических спектров a-частиц совместно с исследованием сопровождающего g‑излучения позволяет построить систему уровней возбужденного ядра.

 Экспериментально было установлено, что наблюдается регулярная связь между периодом полураспада и кинетической энергией испускаемых α-частиц. Период полураспада α-активных ядер тем больше, чем меньше кинетическая энергия испускаемых a-частиц. Однако, если кинетическая энергия Ta a-частиц изменяется в пределах 4 - 9 МэВ, то диапазон изменения периодов полураспада составляет 5·1015 лет ÷ 10-7 с.
Экспериментально было установлено, что наблюдается регулярная связь между периодом полураспада и кинетической энергией испускаемых α-частиц. Период полураспада α-активных ядер тем больше, чем меньше кинетическая энергия испускаемых a-частиц. Однако, если кинетическая энергия Ta a-частиц изменяется в пределах 4 - 9 МэВ, то диапазон изменения периодов полураспада составляет 5·1015 лет ÷ 10-7 с.
Тщательное измерение средней длины Rα пробега в воздухе α-частиц, испускаемых различными веществами, и сопоставление ее с постоянными распада λ этих веществ позволило Г. Гейгеру и Дж. Неттолу в 1911г. получить эмпирическое соотношение
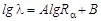
| (3.4.12) |
известное как закон Гейгера – Неттола. Константа А оказалась примерно постоянной для всех трех известных в то время радиоактивных семейств, а константа В отличалась одна от другой примерно на 5% при переходе от одного семейства к другому. Закон Гейгера –Неттола изображен графически на рис. 3.4.3. Прямая 1 соответствует семейству урана, прямая 2 – семейству тория, прямая 3 – семейству актиноурана.. Константа А одинакова для всех семейств, а константа В отличается одна от другой примерно на 5 %. Если использовать связь между пробегом и энергией, устанавливаемую формулой (3.4.11), то закон Гейгера-Неттола можно записать в другой форме:
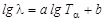 , ,
| (3.4.13) |
 где константы а и b имеют тот же смысл. Выражение (3.4.13) представляет степенную зависимость постоянной распада λ от Тα с очень большим показателем а. Поэтому вероятность α-распада чрезвычайно чувствительна к энергии Qα, выделяемой при распаде. При уменьшение этой энергии на 1 % постоянная распада λ уменьшается более чем в 10 раз, а уменьшение энергии на 10 % приводит к ее уменьшению более чем в 103 раз.
где константы а и b имеют тот же смысл. Выражение (3.4.13) представляет степенную зависимость постоянной распада λ от Тα с очень большим показателем а. Поэтому вероятность α-распада чрезвычайно чувствительна к энергии Qα, выделяемой при распаде. При уменьшение этой энергии на 1 % постоянная распада λ уменьшается более чем в 10 раз, а уменьшение энергии на 10 % приводит к ее уменьшению более чем в 103 раз.
Возникает вопрос, почему энергетически выгодный процесс α-распада, в результате которого высвобождается энергия, не происходит мгновенно, а подчиняется закону Гейгера–Неттола?
Эти особенности α-распада были объяснены в 1929 – 1929 гг. Гамовым, Генри и Кондоном на основе квантовой механики. Если представить a-частицу как целое у границы материнского ядра, то она должна занимать уровень с положительной энергией, равной Тα (рис. 3.4.4) и для того, чтобы стать свободной, должна переместиться а точку RA. Но у тяжелых ядер высота кулоновского барьера (Вc на рис. 3.4.4) составляет около 30 МэВ для двухзарядной точечной частицы (см. (1.9.2)). Барьер для α-частицы конечных размеров несколько ниже и составляет 22 ÷ 25 Мэв. Преодоление α-частицей с кинетической энергией 4 ÷ 9 Мэв даже такого барьера по классическим представлениям невозможно. Однако, согласно квантовым законам, при любой конечной ширине барьера падающая на него частица с положительной энергией имеет, хотя и малую, но конечную вероятность D «просочиться» сквозь барьер. Величину D часто называют прозрачностью барьера.
Вероятность вылета α-частицы из ядра в единицу времени или постоянная распада λ будет равна числу попыток k в единицу времени пройти сквозь барьер, умноженную на вероятность D просачивания сквозь потенциальный барьер при одном столкновении со стенкой:
| l = kD. | (3.4.14) |
Число попыток в единицу времени k = Р·ν,где Р - вероятность образования α-частицы из двух протонов и двух нейтронов ядра, так как в готовом виде α-частиц в ядре нет, а ν – частота соударений образующейся α-частицы со стенками ядра. Вычисление величины Р является сложной и пока не решенной до конца задачей ядерной физики. Обширный экспериментальный материал позволяет заключить, что 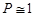 для четно-четных ядер в основном и слабо возбужденных состояниях. Если теперь представить, что α-частица движется внутри сферического ядра радиусом R со скоростью vα, то частота ударов ν со стенкой потенциальной ямы составит vα/2R. Аппарат квантовой механики приводит к следующему выражению для коэффициента D прозрачности потенциального барьера, равного отношению потоков частиц на границах барьера и дающего меру вероятности оказаться частице за пределами потенциального барьера при столкновении с его стенкой:
для четно-четных ядер в основном и слабо возбужденных состояниях. Если теперь представить, что α-частица движется внутри сферического ядра радиусом R со скоростью vα, то частота ударов ν со стенкой потенциальной ямы составит vα/2R. Аппарат квантовой механики приводит к следующему выражению для коэффициента D прозрачности потенциального барьера, равного отношению потоков частиц на границах барьера и дающего меру вероятности оказаться частице за пределами потенциального барьера при столкновении с его стенкой:
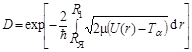 . .
| (3.4.15) |
В этом выражении 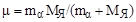 - приведенная масса a-частицы и дочернего ядра, а пределами интегрирования являются границы барьера (см. рис. 3.4.3), т.е. область, классически недоступная для движения a-частицы.
- приведенная масса a-частицы и дочернего ядра, а пределами интегрирования являются границы барьера (см. рис. 3.4.3), т.е. область, классически недоступная для движения a-частицы.
Подставив (3.4.15) в (3.4.14) и логарифмируя, получим, что
| lgl =lg k + φ(Тα), | (3.4.16) |
где
·φ(Тα) = 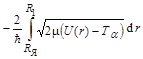 , ,
| (3.4.17) |
Полученное выражение (3.4.16) для всех тех значений Тα, которые встречаются у α-частиц естественных радиоактивных нуклидов, сходно с законом Гейгера-Неттола (3.4.13) и по форме и по содержанию. Следует заметить, что формула (3.4.16) хорошо описывает связь периода постоянной распада и кинетической энергией α-частиц только для четно-четных ядер. Для нечетно-нечетных ядер экспериментальные точки не ложатся на кривую, даваемую зависимостью (3.4.16).
Из курса механики известно, что кинетическая энергия Т материальной точки может быть представлена как сумма кинетической энергии Тп поступательного (радиального) движения и кинетической энергии Твр вращательного движения относительно некоторой оси, проходящей через точку начала координат. До сих пормолчаливо предполагалось, что a-частица вылетает из ядра по радиальному направлению относительно центра инерции материнского ядра и ее орбитальный момент l = 0. В этом случае высвобождаемая при α-распаде энерги Еα полностью переходит в кинетическую энергию поступательного движения продуктов распада (если энергия вобуждения дочернего ядра равна нулю). Если же a-частица имеет относительно центра инерции ядра некоторый орбитальный момент l > 0, то в этом случае кинетическая энергия 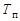 ее поступательного движения, необходимая для преодоления кулоновского барьера, уменьшится на величину энергии вращательного движения системы относительно центра инерции ядра. Это означает, что
ее поступательного движения, необходимая для преодоления кулоновского барьера, уменьшится на величину энергии вращательного движения системы относительно центра инерции ядра. Это означает, что 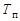 = Тα - Твр, и a-частица, кроме кулоновского, должна преодолевать т.н. центробежный барьер
= Тα - Твр, и a-частица, кроме кулоновского, должна преодолевать т.н. центробежный барьер
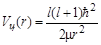 . .
| (3.4.19) |
Т.о. центробежная энергия увеличивает протяженность потенциального барьера U(r) в (3.4.15), уменьшая вероятность распада. Искажение формы потенциального барьера за счет центробежной энергии незначительно из-за того, что центробежная энергия спадает значительно быстрее кулоновской (как r-2, а не как r-1). В таблице 3.4.1 приведен коэффициент η уменьшения вероятности распада для различных орбитальных моментах l, уносимой a-частицей, при типичных значениях Tα = 5 МэВ и RЯ = 9,6·10-13 см.
Таблица 3.4.1
| l | ||||||
| η | 0,85 | 0,60 | 0,35 | 0,18 | 0,08 |
При этом следует иметь в виду, что допустимые значения l ограничены законом сохранения спина (см. §4.4)
| |Iм – Iд| ≤ l ≤ Iм + Iд, | (3.4.20) |
где Iм и Iд - спины материнского и дочернего ядер соответственно, и законом сохранения четности. В (3.4.20) l должно быть четным, если четности материнского ядра совпадают, и нечетным, если эти четности различны.
Кроме этого на вероятность a-распада влияет несферичность ядра (все α-активные ядра имеют устойчивую эллипсоидальную форму), оболочечная структура ядра, искажение кулоновского барьера полем электронной оболочки, закругление вершины кулоновского барьера (конечные размеры α-частицы) и ряд других факторов. Теория α-распада еще далека от совершенства и работы по уточнение теории a-распада продолжаются и в настоящее время.
Бета – распад
Стабильные атомные ядра изобаров имеют минимальную величину энергии, которая определяется его массой (см. рис. 2.2.1). Масса ядра с данным общим числом нуклонов определяется, в свою очередь, его протонно-нейтронным составом, поскольку массы протона и нейтрона не равны между собой. В этой связи, среди ядер изобаров должны существовать ядра с определенным соотношением между числом протонов и нейтронов (см. дорожку стабильности на рис. 1.1.2), которому отвечают ядра с наименьшей массой, а, следовательно, и полной энергией. Ядру изобара с любой другой конфигурацией нуклонного состава энергетически выгодно превращение в ядро с оптимальным соотношением между числом протонов и нейтронов. Выход на дорожку стабильности в принципе возможен, если ядро испускает избыточный протон или нейтрон. Но для отделения избыточного нуклона требуется энергия не меньше энергии связи нуклона в ядре, т.е. энергия материнского ядра должна быть больше энергии дочернего ядра и свободного нуклона на величину энергии связи нуклона в материнском ядре. Если же эта энергия меньше энергии связи избыточного нейтрона в ядре, то могут иметь место самопроизвольные изменения в составе ядер, обусловленные явлением b-распада – взаимопревращением внутри ядра нуклонов одного рода в другой (протона в нейтрон или наоборот). Направление процесса для ядра изобара определяется лишь тем, при каком соотношении между числом протонов и нейтронов ядро имеет наибольшую энергию связи, которой соответствует наименьшая масса ядра (см. рис. 2.2.1).
Бета-распад (b-распад) является спонтанным процессом преобразования ядра, в результате которого ядро изменяет свой заряд на ΔΖ = ±1, сохраняя при этом неизменное число нуклонов А (массовое число). В некоторых случаях образуются свободные b-частицы (электрон β-или позитрон β+) или происходит «захват» ядром электрона из электронной оболочки собственного атома. Свойства электрона и позитрона тождественны, за исключением знака электрического заряда. Потоки образующихся b-частиц образуют b-излучение.
β-Распад – самый распространенный вид радиоактивных превращений ядер в природе. В отличие от α-распада, который наблюдается исключительно у тяжелых ядер, β-распаду подвержены ядра практически во всей области значений массового числа А, начиная от единицы (свободный нейтрон) и заканчивая массовыми числами самых тяжелых ядер.
Энергия, выделяющаяся при β-распаде, опять же, в отличие от α-распада, лежит в довольно широком интервале значений от 0,02 МэВ прираспаде ядра трития 3Н до 16,4 МэВ при распаде ядра 12N.
Периоды полураспада β-активных ядер изменяются в очень широких пределах от 10-2 с до 1018 лет.
Известны три разновидности b-распада.
1. Электронный (β-- распад):
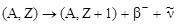 , ,
| (3.5.1) |
при котором выбрасываются электрон β- и антинейтрино 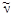 , а дочернее ядро получает заряд на единицу больший, чем материнское, так как в ядре уменьшается число нейтронов на единицу за счет увеличения на единицу числа протонов. Например:
, а дочернее ядро получает заряд на единицу больший, чем материнское, так как в ядре уменьшается число нейтронов на единицу за счет увеличения на единицу числа протонов. Например:
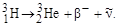
|
2. Позитронный (b+ - распад):
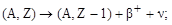
| (3.5.2) |
при котором выбрасываются позитрон β+ и нейтрино ν, а дочернее ядро получает заряд на единицу меньший, чем материнское, так как в ядре увеличивается на единицу число нейтронов из-за уменьшения на единицу числа протонов. Например:
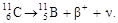
|
3. E-захват (или К-захват - по обозначению электронной оболочки, с которой чаще всего захватывается электрон):
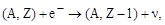
| (3.5.3) |
где е- - атомный электрон. В результате Е-захвата один из электронов, как правило, один из двух самой глубокой К-оболочки атома, захватывается ядром. При этом выбрасывается нейтрино ν, а дочернее ядро получает заряд на единицу меньше, чем материнское. Например:
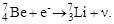
|
Е-захват и b+ - распад часто конкурируют между собой, так как в этих случаях материнские ядра претерпевают одинаковые изменения.
Таким образом, при b-распаде любого вида число нуклонов в ядре сохраняется, но происходит самопроизвольное превращение либо нейтрона в протон (β-- распад), либо протона в нейтрон (b+-распад и Е-захват). Именно поэтому Е-захват относится к процессам b-распада.
Так как при b-распаде изменяется только один из нуклонов ядра, то этот процесс – внутринуклонный, а не внутриядерный. Подтверждением этому служит b-распад свободного нейтрона, протекающего по следующей схеме:
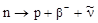 . .
| (3.5.4) |
Современное значение периода полураспада нейтрона составляет 10,25 мин. (1988 г.).
Превращение (b+-распад) свободного протона в нейтрон запрещено законом сохранения энергии, так как его масса на 1,3 МэВ меньше массы нейтрона. Но в составе ядра он может преоб
Дата добавления: 2021-07-22; просмотров: 1042;











