Спин, магнитный и электрический моменты ядер
Спин ядра
Ядро, как пространственно ограниченная и связанная система взаимодействующих между собой нуклонов, в определенных случаях может рассматриваться в целом как одна микрочастица. Так как нуклоны, из которых состоит ядро, обладают собственным механическим моментом, или спином, а также совершают движение относительно друг друга (орбитальное движение относительно центра инерции ядра), то и ядра должны иметь собственный механический момент (далее просто момент) или спин.
Спин ядра 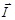 есть векторная сумма полных моментов
есть векторная сумма полных моментов 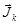 отдельных нуклонов, каждый из которых складывается из орбитального момента
отдельных нуклонов, каждый из которых складывается из орбитального момента 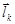 и собственного момента (спина) нуклона
и собственного момента (спина) нуклона 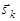 , так что
, так что
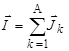 , а , а 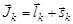 . . 
| (1.6.1) |
Возможна другая схема сложения моментов отдельных нуклонов, дающая другой результат, когда сначала отдельно суммируются векторы спинов, а затем векторы орбитальных моментов всех нуклонов, и полученные два вектора складываются. Однако, поскольку ядерные силы не центральны (см. §1.9 п.7) и в ядре существует спин-орбитальное взаимодействие (см. §2.3 п.1), то по этой причине в теории ядра используют первую схему.
Естественной единицей измерения момента импульса в квантовой механике служит постоянная Планка ħ = 1,0546·10-34 Дж·с, имеющая размерность момента импульса.
Вектор момента любых микрочастиц, как, впрочем, и спин ядра, обладает своеобразными свойствами.
1. Абсолютная величина вектора момента любой изолированной физической величины может принимать только дискретные значения:
| 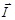 | | 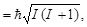
| (1.6.2) |
где I – положительное число, либо целое, либо полуцелое:
| I = 0, 1/2, 1, 3/2, ... | (1.6.3) |
Число I называют обычно величиной момента или квантовым числом момента. Следует особо отметить различие между модулем вектора 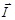 и квантовым числом I, так как последнее является одним из чисел (1.6.3), используемых в формуле (1.6.2) для нахождения модуля вектора
и квантовым числом I, так как последнее является одним из чисел (1.6.3), используемых в формуле (1.6.2) для нахождения модуля вектора 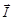 . Когда говорят: «момент 1/2», то имеют в виду именно это квантовое число в формуле (1.6.2). Нуклоны (и электрон тоже) имеют квантовое число спина s = 1/2 (спин равен 1/2).
. Когда говорят: «момент 1/2», то имеют в виду именно это квантовое число в формуле (1.6.2). Нуклоны (и электрон тоже) имеют квантовое число спина s = 1/2 (спин равен 1/2).
В формуле (1.6.1) квантовое число lk для орбитального момента всегда целое число, lk = 0, 1, 2, и т.д.
2. Мгновенное значение вектора механического момента любой микрочастицы не имеет смысла по той же причине, по которой в квантовой механике не имеет смысла мгновенное значение вектора импульса. Строго фиксированное значение может иметь только абсолютная величина вектора момента (1.6.2) и одна из его пространственных проекций, обычно называемой проекцией на ось Z, которая обозначается как Iz. Проекция момента Iz может принимать случайным образом одно из (2I + 1) значений, уменьшающихся на единицу:
| Iz = Iћ, (I – 1)ћ, . . . , -Iћ. | (1.6.4) |
Реализация любой возможной проекции из набора (1.6.4) оказывается равновероятной.
Число возможных проекций на ось Z четно, если I – полуцелое число, и нечетно, если I – целое число. Знак плюс или минус в (1.6.4) означает ориентацию вектора момента на выбранное направление оси Z в пространстве. Однако величины проекций Ix и Iy оказываются совершенно неопределенными[1]и флуктуируют относительно нулевого среднего значения. Учитывая, что
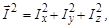
| (1.6.5) |
имеем
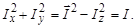
| (1.6.6) |
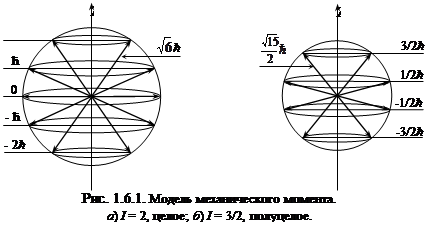 Таким образом, квадраты проекций вектора момента на оси Х и Y не равны нулю. По этой причине проекция момента Iz всегда меньше абсолютной величины вектора механического момента, т.е. направление вектора
Таким образом, квадраты проекций вектора момента на оси Х и Y не равны нулю. По этой причине проекция момента Iz всегда меньше абсолютной величины вектора механического момента, т.е. направление вектора 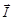 никогда не может совпадать с осью Z. Действительно, согласно (1.6.4), максимальное значение
никогда не может совпадать с осью Z. Действительно, согласно (1.6.4), максимальное значение 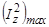 =
= 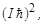 тогда как согласно (1.6.2)
тогда как согласно (1.6.2) 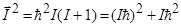 . Все перечисленные выше свойства вектора механического момента обычно демонстрируют с помощью квазиклассической модели (рис. 1.6.1), которая находится в определенном согласии со свойствами квантовомеханического вектора момента. Вектор момента, величина которого вычисляется с помощью (1.6.2), прецессирует относительно оси Z с некоторой угловой скоростью и может ориентироваться вдоль или против направления оси Z только таким образом, чтобы его проекция на ось Z была равна одному из значений от +Iћ до –Iћ через единицу. Этот вектор никогда не может ориентироваться точно по направлению оси Z, поскольку его величина, как отмечено выше, не равна Iћ. Поэтому, помимо величины вектора момента, сохраняющейся во времени величиной является только одна проекция вектора – проекция на ось Z. Полное число проекций Iz вектора момента на рис.1.6.1 равно (2I + 1).
. Все перечисленные выше свойства вектора механического момента обычно демонстрируют с помощью квазиклассической модели (рис. 1.6.1), которая находится в определенном согласии со свойствами квантовомеханического вектора момента. Вектор момента, величина которого вычисляется с помощью (1.6.2), прецессирует относительно оси Z с некоторой угловой скоростью и может ориентироваться вдоль или против направления оси Z только таким образом, чтобы его проекция на ось Z была равна одному из значений от +Iћ до –Iћ через единицу. Этот вектор никогда не может ориентироваться точно по направлению оси Z, поскольку его величина, как отмечено выше, не равна Iћ. Поэтому, помимо величины вектора момента, сохраняющейся во времени величиной является только одна проекция вектора – проекция на ось Z. Полное число проекций Iz вектора момента на рис.1.6.1 равно (2I + 1).
3. Модуль вектора момента 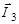 сложной системы, составленной из двух подсистем с моментами
сложной системы, составленной из двух подсистем с моментами 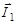 и
и 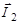 , вычисляется из выражения
, вычисляется из выражения
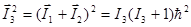 
| (1.6.7) |
обычным образом через свои квантовые числа 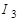 . Сложение векторов
. Сложение векторов 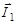 и
и 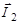 есть сложение их проекций как алгебраических чисел. Для получения всех возможных проекций вектора
есть сложение их проекций как алгебраических чисел. Для получения всех возможных проекций вектора 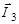 на ось Z каждая из проекций вектора
на ось Z каждая из проекций вектора 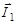 складывается с каждой из проекций вектора
складывается с каждой из проекций вектора 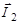 . Таких проекций вектора
. Таких проекций вектора 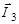 оказывается всего (2I1 + 1)(2I2 + 1), которые будут образовывать (2Im + 1) векторов
оказывается всего (2I1 + 1)(2I2 + 1), которые будут образовывать (2Im + 1) векторов 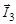 , Im = min{I1,I2}, со следующими значениями квантовых чисел:
, Im = min{I1,I2}, со следующими значениями квантовых чисел:
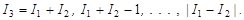 
| (1.6.8) |
Соотношение (1.6.8) определяет правило сложения моментов в квантовой механике.
Поскольку каждое значение проекции из (2I1 + 1)(2I2 + 1) возможных реализуется с равной вероятностью, то относительная вероятность образования состояния со спином 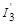 из возможного набора значений (1.6.8) составит
из возможного набора значений (1.6.8) составит
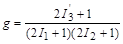 , , 
| (1.6.9) |
т.е. равна отношению числа возможных проекций вектора 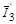 к полному числу проекций возможных значений вектора
к полному числу проекций возможных значений вектора 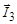 . Величина g называется статистическим фактором или статистическим весом.
. Величина g называется статистическим фактором или статистическим весом.
4. Любая векторная величина 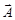 , характеризующая физические свойства микрочастицы, пропорциональна вектору момента
, характеризующая физические свойства микрочастицы, пропорциональна вектору момента 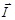 :
:
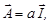 
| (1.6.10) |
где а – константа, полностью характеризующая вектор.
В отношении спинов различных ядер наблюдаются следующие опытные закономерности:
а) Для ядер с четными А спины всегда целые, а при нечетном А – всегда полуцелые.
б) Четно-четные ядра (А - четное) в основном состоянии имеют спин равный нулю. Этот факт дает основания полагать, что одноименные нуклоны с одинаковыми величинами, но противоположно направленными векторами 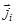 полных моментами, объединяются в пары (эффект спаривания, см. §1.4 п.3) и суммарный момент импульса ядра оказывается равным нулю.
полных моментами, объединяются в пары (эффект спаривания, см. §1.4 п.3) и суммарный момент импульса ядра оказывается равным нулю.
в) Нечетно-нечетные ядра (А - четное) имеют целочисленный спин. Это указывает на то, что разноименные нуклоны объединяются в пары с одинаковым направлением векторов механического момента, создавая целочисленный момент (см. §1.11).
г) Ядра с нечетным А имеют полуцелый спин в пределах от 1/2 до 9/2, что крайне мало по сравнению с суммой абсоютных значений полных моментов 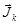 (см. (1.6.1)) отдельных нуклонов для большинства ядер. По-видимому векторы
(см. (1.6.1)) отдельных нуклонов для большинства ядер. По-видимому векторы 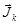 полных механических моментов для большинства одноименных нуклонов попарно компенсируются и не участвуют в создании спина ядра.
полных механических моментов для большинства одноименных нуклонов попарно компенсируются и не участвуют в создании спина ядра.
Дата добавления: 2021-07-22; просмотров: 614;











