Течение жидкости по закону Дарси к несовершенной скважине
Течение жидкости по закону Дарси кнесовершенной скважине по степени вскрытия, а также по характеру вскрытия изучалась В. И. Щуровым путём электролитического моделирования. Он построил опытные диаграммы зависимости С от параметра a=h/D ( h – толщина пласта, D– диаметр скважины) и относительного вскрытия пласта `h=hвс/h (hвс – толщина вскрытия ). Таким же методом исследовалась несовершенная по характеру вскрытия скважина Доуэллом и Маскетом, а также Ховардом и Ватсоном. В результате получены зависимости коэффициента несовершенства от плотности перфорации (числа отверстий на 1погонный метр колонны труб) и глубины прострела, которые показали значительную зависимость дебита от плотности перфорации только до значений 16 – 20 отверстий на 1 погонный метр.
Для несовершенной по степени вскрытия пласта скважины на основе метода суперпозиции и отображения стоков М. Маскетом получена зависимость для дебита:
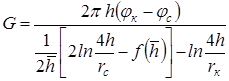 , (11.5)
, (11.5)
где f – функция относительного вскрытия имеет вид (рисунок 11.2) и определяется выражением:
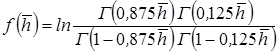 , (11.6)
, (11.6)
где Г – табулированная гамма – функция или интеграл Эйлера второго рода.
Если глубина вскрытия не слишком мала, то формула Маскета даёт хорошие результаты. Ею нередко пользуются для скважин, несовершенных по степени вскрытия, но совершенных по характеру вскрытия.
Из зависимости (11.5) видно, что коэффициент несовершенства по степени вскрытия С можно выразить зависимостью:
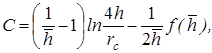 (11.7)
(11.7)
и он добавляется к фильтрационному сопротивлению совершенной скважины.
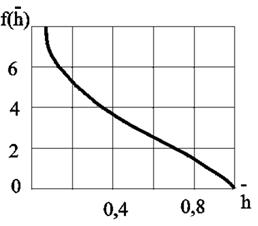
Рисунок 11.2 – График функции 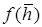
Если толщина пласта много больше радиуса скважины, то для расчета дебитов несовершенной по степени вскрытия скважины можно пользоваться более простой формулой Н. К. Гиринского:
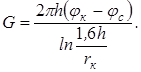 (11.8)
(11.8)
Если скважины ещё и несовершенны по характеру вскрытия, то коэффициент Сувеличивается на величину сопротивления фильтра:
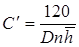 , (11.9)
, (11.9)
где D – диаметр фильтрового отверстия в см; n – число отверстий на 1 м перфорированной части.
11.3 Течение реального газа по двухчленному закону к несовершенной скважине
В большинстве случаев дебит газовых скважин не следует закону Дарси, так же как в некоторых случаях и дебит нефтяных или водяных скважин.
Вблизи фильтрационных отверстий при приближении к стенке скважины скорость фильтрации становится настолько большой, что число Рейнольдса превосходит критическое. Квадраты скоростей становятся настолько большими, что ими пренебрегать уже нельзя.
Для случая фильтрации газа Е. М. Минским и П. П. Марковым доказана сильная нелинейная зависимость коэффициентов фильтрации от относительного вскрытия пласта.
Уравнение притока реального газа по двухчленному закону фильтрации к совершенной скважине записывается в виде, аналогично идеальному:
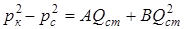 , (11.10)
, (11.10)
но здесь А и В являются функциями давления р и температуры Т:
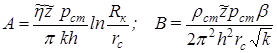 . (11.11)
. (11.11)
Приток к несовершенной скважине учитывается так же как и при фильтрации по закону Дарси, т. е. введением приведённого радиуса скважины 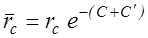 в формулу дебита.
в формулу дебита.
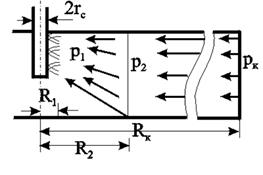
Рисунок 11.3 – Схема притока газа к несовершенной по степени и по характеру вскрытия скважине
При нарушении закона Дарси для скважины несовершенной по степени и характеру вскрытия для расчета притока используют следующую схему. Пласт делится на три области. Первая область имеет радиус R1» (2–3) rc. Здесь из-за больших скоростей вблизи перфорации происходит нарушение закона Дарси и проявляется в основном несовершенство по характеру вскрытия. Вторая область кольцевая с R1< r< R2 и R2» h. Здесь линии тока искривляются из-за несовершенства по степени вскрытия и фильтрация происходит тоже по двухчленному закону. В третьей области (R2< r< Rк) действует закон Дарси и течение плоскорадиально.
Для третьей области:
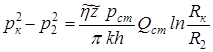 . (11.12)
. (11.12)
Во второй области толщина пласта рассматривается как изменяющаяся по линейному закону от hвс при r = R1 до h при r = R2 (hвс – глубина вскрытия), т. е. h(r)=a+b r, где a и b определяются из условий h(r)=hвс при r = R1 и h(r)= h при r = R2. Чтобы получить закон движения в этой области, надо проинтегрировать уравнение (11.10), предварительно подставив вместо постоянной толщины h переменную h(r), и, учтя реальные свойства газа:
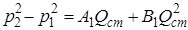 , (11.13)
, (11.13)
где
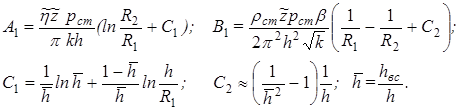 ,
,
С2– вычисляется приближенно в области hвс>> R1.
В первой области фильтрация происходит по двухчленному закону, и плоскорадиальное течение нарушается из-за перфорационных отверстий. Уравнение притока имеет вид (11.13), но несовершенство учитывается коэффициентами С3 и С4, а R2заменяется на R1 и R1 – на rc.
Коэффициент С3определяется по графикам Щурова, а для С4 предлагается приближенная формула:
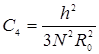 , где N– суммарное число отверстий; R0 – глубина проникновения перфорационной пули в пласт.
, где N– суммарное число отверстий; R0 – глубина проникновения перфорационной пули в пласт.
Складывая почленно уравнение притока для этих областей, получим уравнение притока для несовершенной скважины:
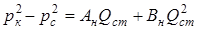 , (11.14)
, (11.14)
где
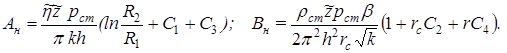
Дата добавления: 2017-06-13; просмотров: 2012;











