Виды несовершенств скважин. Приведённый радиус. Добавочное фильтрационное сопротивление

Гидродинамическое несовершенство скважины проявляется в том, что в призабойной зоне пласта с конечной толщиной отсутствует радиальность потока, обусловленная конструкцией забоя или фильтра.

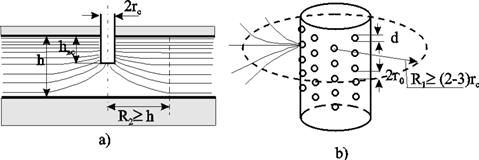
Рисунок 11.1 – Схема притока к несовершенной скважине: а) по степени вскрытия; b) по характеру вскрытия

Различают несовершенство по степени вскрытия и несовершенство по характеру вскрытия.

Несовершенная скважина по степени вскрытия – это скважина с открытым забоем, вскрывшая пласт не на всю мощность, а частично (рисунок 11.1а).

Скважина, хотя и доведённая до подошвы пласта, но сообщающаяся с пластом только через отверстия в колонне труб, в цементном кольце или в специальном фильтре, называется несовершенной по характеру вскрытия пласта (рисунок 11.1b).

На практике чаще встречаются скважины несовершенные как по степени, так и по характеру вскрытия пласта.

Дебит G несовершенной скважины меньше дебита G_с совершенной, действующей в тех же условиях, что и данная несовершенная скважина. В некоторых случаях (при торпедной или кумулятивной перфорации, когда глубина прострела достаточно велика) может наблюдаться обратная картина. Отношение данных дебитов d характеризует степень несовершенства скважины и называется коэффициентом несовершенства:

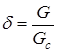. (11.1)

Коэффициент несовершенства зависит от :

от относительного вскрытия пласта ,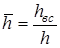

где h_вс – глубина погружения скважины в пласт , h – толщина пласта;

от числа отверстий, приходящихся на 1м колонны, размеров и формы отверстий;

от глубины прострела.

При расчете несовершенных скважин нередко используют понятие приведенного радиуса несовершенной скважины:

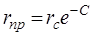. (11.2)

Приведенный радиус – это радиус такой совершенной скважины, дебит которой равняется дебиту данной несовершенной скважины при тех же условиях эксплуатации. Обычно вычисляются приведённые радиусы r_пр и дальнейший расчет несовершенных скважин ведется как для совершенных скважин радиуса r_пр.

Влияние несовершенства скважины на приток при существовании закона фильтрации Дарси можно учесть величиной коэффициента С, основываясь на электрической аналогии. Согласно данной аналогии различие в дебитах совершенной G_c и несовершенной Gскважин объясняется наличием добавочного фильтрационного сопротивления несовершенной скважины величиной С/2ph, т. е. дебит несовершенной скважины можно представить в виде:

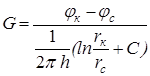. (11.3)

Зависимость между коэффициентом d и величиной Стакова:

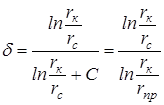. (11.4)