Приток к прямолинейной батарее скважин

Рассмотрим приток к прямолинейной батарее скважин при удалённом контуре питания в режиме поддержания постоянного забойного давления. Необходимо различать два случая: число скважин батареи нечетное; число скважин четное. В обоих случаях дебиты скважин, равноудаленные от середины или от концов батареи, будут одинаковы, а при разной удаленности будут отличаться. Последнее вызывается не одинаковой интенсивностью влияния со стороны скважин батареи на те или иные скважины. При нечетном числе скважин дебит средней скважины отличается от дебитов других скважин.

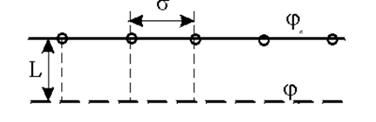
Рисунок 10.4 – Схема прямолинейной батареи скважин

Дебиты равномерно расположенных скважин можно определить общим методом с использованием формулы (9.2).

Для практических расчетов можно использовать приближенную формулу П. П. Голосова для общего дебита скважин прямолинейной батареи:

для нечетного числа скважин 2n+1, где n – любое целое число:

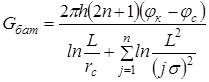
; (10.12)

для четного числа скважин 2n:

. (10.13)

Здесь h – толщина пласта; s – расстояние между скважинами; L – расстояние до контура питания.

Ошибка в определении дебитов по этим формулам не превышает 3 – 4 % при L=10 км,r_с=10 см и расстояниях между скважинами 100 м£ s £ 500 м.

Приведенные формулы можно использовать при любом контуре питания, т. к. проведенные ранее исследования взаимодействия двух скважин показали, что форма контура питания пласта мало влияет на взаимодействие скважин. Что касается расстояния скважин до контура питания, то по мере приближения скважин к контуру питания эффект взаимодействия уменьшается, но в реальных условиях значительного удаления скважин от контура питания погрешность определения расстояния до контура даже в 100 % не отражается значительно на эффекте взаимодействия. Для однородных пластов и жидкостей относительные изменения дебитов скважин, вызванные эффектом взаимодействия, не зависят от физико - геологических характеристик пласта и от физических параметров жидкости.

Рассмотрим фильтрационное поле (рисунок 10.5), поддерживаемое, бесконечной цепочкой равностоящих скважин (это требование приводит к ликвидации граничных эффектов на концах батареи и равнодебитности скважин, т. к. все скважины оказываются в равных условиях притока к ним).

Используя формулу дебита скважины кольцевой батареи, получим формулу массового дебита скважины прямолинейной батареи:

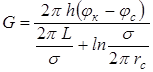. (10.14)

Здесь L – расстояние от контура питания до батареи; s – расстояние между скважинами батареи; h – толщина пласта.

Суммарный дебит n скважин определится выражением:

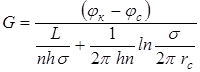. (10.15)

Для несжимаемой жидкости соотношение (10.15) можно переписать через давление и объёмный дебит:

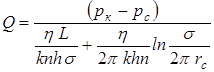. (10.16)

Ортогональная сетка, изображающая фильтрационное поле бесконечной прямолинейной батареи, изображена на рисунке 10.5 .

Здесь, как и в кольцевой батарее, имеются главные и нейтральные линии тока, перпендикулярные цепочке. Нейтральными линиями тока вся плоскость течения делится на бесконечное число полос, каждая из которых является полосой влияния одной из скважин, находящейся в середине расстояния между двумя соседними нейтральными линиями. Главные линии тока проходят через центры скважин, параллельно нейтральным линиям.

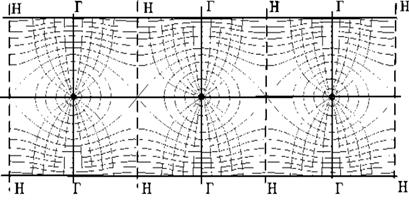
Рисунок 10.5 – Фильтрационное поле при бесконечной цепочке скважин

Изобара, бесчисленное множество раз пересекающая сама себя, отделяет изобары внешнего течения ко всей батареи, охватывающих всю цепочку скважин, от изобар притока к скважине, охватывающих только данную скважину. Точки пересечения граничной изобары являются точками равновесия, и они делят интервал между двумя соседними скважинами пополам.

10.4 Метод эквивалентных фильтрационных сопротивлений

Данный метод Ю. П. Борисова позволяет сложный фильтрационный поток в пласте при совместной работе нескольких батарей эксплуатационных и нагнетательных скважин разложить на простейшие потоки – к одиночно работающей скважине и к одиночно работающей батарее. Реализация данного метода достигается введением понятий внутреннего и внешнего фильтрационных сопротивлений, которые придают простой физический смысл членам уравнений, используемых для подсчетов дебитов и значений потенциальных функций. Для выяснения этих понятий сравним формулы (10.15) или (10.16) с законом Ома I = U / R, где I – ток, U – разность потенциалов и R – сопротивление. Из сравнения видно, что фильтрационное сопротивление определяется величиной знаменателя правой части (10.15), который состоит из двух слагаемых. Если в (10.15) оставить только первое слагаемое, то оно будет выражать дебит в прямолинейно-параллельном потоке через площадь величиной nhs на длине L. Первое слагаемое выражает фильтрационное сопротивление потоку от контура питания к участку прямолинейной бесконечной цепочки, занятому n скважинами, в предположении замены батареи галереей. Б. Борисов назвал эту часть фильтрационного сопротивления внешним:

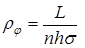
или 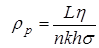. (10.17)

Оставим теперь в (10.15) только второе слагаемое. В этом случае получим аналог формулы Дюпюи для суммарного дебита n скважин при плоскорадиальном течении и в предположении, что каждая скважина окружена контуром питания длиной s. Второе слагаемое выражает местное фильтрационное сопротивление, возникающее при подходе жидкости к скважинам. Появление этого сопротивления объясняется искривлением линий тока у скважин и Ю. Борисов назвал его внутренним:

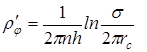
или

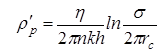. (10.18)

На внешнее и внутреннее фильтрационные сопротивления разделяется также полное фильтрационное сопротивление кольцевой батареи:

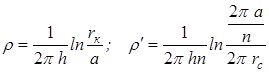
. (10.19)

Здесь r выражает фильтрационное сопротивление потоку от контура питания к кольцевой батарее радиуса а в предположении, что поток плоскорадиален и батарея заменена галереей. Внутреннее сопротивление r^/ есть сопротивление плоскорадиального потока от воображаемого контура окружности длиной 2pа/n к скважине. Величина 2pа/n – длина дуги сектора радиуса а, который содержит одну из скважин батареи. Электрическая схема в случае одной батареи имеет вид (рисунок 10.6). На рисунке 10.6 затемнены области внутреннего сопротивления.

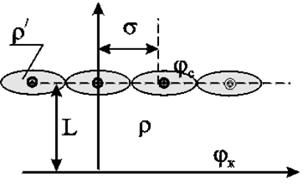
Рисунок 10.6 – Схема одной батареи