Приток к группе скважин с удаленным контуром питания

В большинстве практических случаев контур питания находится довольно далеко от групп скважин.

Пусть в пласте расположена группа из n скважин (рисунок 10.1) с различными дебитами G_i, забойными потенциалами j_iи радиусами скважин r_i. Расположение скважин задано и на достаточно большом удалении находится контур питания, форма которого неизвестна, но известен порядок расстояния r_к от контура питания до группы скважин. При этом r_к намного больше расстояния между скважинами. Считаем, что известны потенциал контура j _к и забойные потенциалыскважин j _i.

Для определения дебитов используем формулу (9.2) при помещении точки Мна забое каждой скважины, что позволяет записать n уравнений вида:

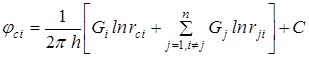, (10.1)

где r_ci– радиус скважины на которую помещена точка М; r_ji– расстояние между i - й и j - й скважинами; j_ci – забойный потенциал i- й скважины.

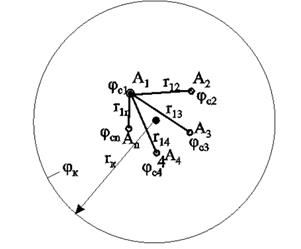
Рисунок 10.1 – Схема группы скважин в пласте

с удалённым контуром питания

Неизвестных же n+1, так как константа тоже неизвестна. Для нахождения константы Своспользуемся условием j = j_к на удалённом контуре питания:

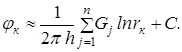(10.2)

Приближение заключается в том, что для удаленных точек контура питания от скважин принимаем одно и тоже расстояние r_к, что справедливо для достаточного удаления контура, учитывая что оно находится под знаком логарифма. Уравнение (10.2) и будет (n+1) уравнением.

Таким образом, плоская задача интерференции при удалённом контуре питания сводится к решению алгебраической системы уравнений первой степени (10.1), (10.2). При ее помощи можно находить или депрессию при заданном дебите, или получить значения дебитов при заданных депрессиях. При найденных дебитах можно определить пластовое давление в любой точке, причем результат будет тем точнее, чем дальше эта точка отстоит от контура питания.