Алгоритм расчета показателей установившегося притока к горизонтальной скважине
Известные методы расчёта притока жидкости к одиночной горизонтальной скважине основаны на аналитических зависимостях между гидропроводностью пласта, депрессией на пласт и геометрией зоны дренирования, которая одними авторами принимается в виде круга или эллипсоида, другими в виде усеченного шара или в форме полосообразного пласта.
Основная задача состоит в том, чтобы рассчитать дебит жидкости горизонтальной скважины на основе различных методов при установившемся режиме фильтрации и построить зависимости, которые позволят увидеть, как влияет толщина пласта, диаметр скважины, длина горизонтального ствола и коэффициент анизотропии на дебит горизонтальной скважины.
Для определения притока к горизонтальной скважине при установившемся режиме фильтрации, наиболее часто используют следующие методы [28]:
1) Метод Борисова, который допускает, что зона, дренируемая горизонтальной скважиной, имеет форму круга:
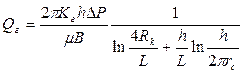 . (1.57)
. (1.57)
2) По Giger, который допускает, что зона дренируемая горизонтальной скважиной по площади, имеет форму усеченного сверху и снизу эллипсоида:
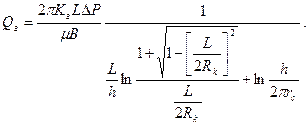 (1.58)
(1.58)
3) Установившийся приток к горизонтальной скважине для эллиптического пласта в зависимости от его длины, можно рассчитать по методу Джоши:
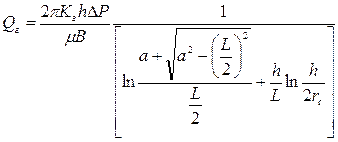 . (1.59)
. (1.59)
4) Метод Ренарда и Дюпии, который допускает, что зона дренируемой горизонтальной скважиной по площади имеет форму эллипса:
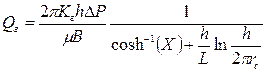 . (1.60)
. (1.60)
В приведенных выражениях:
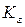 -коэффициент проницаемости по горизонтали;
-коэффициент проницаемости по горизонтали;
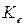 - коэффициент проницаемости по вертикали;
- коэффициент проницаемости по вертикали;
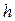 -толщина продуктивного пласта;
-толщина продуктивного пласта;
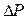 - перепад давления;
- перепад давления;
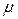 - коэффициент динамической вязкости нефти;
- коэффициент динамической вязкости нефти;
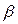 - объемный коэффициент нефти;
- объемный коэффициент нефти;
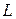 -длина горизонтального ствола;
-длина горизонтального ствола;
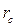 -радиус скважины;
-радиус скважины;
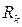 - радиус дренирования для горизонтальной скважины (условный радиус контура питания);
- радиус дренирования для горизонтальной скважины (условный радиус контура питания);
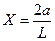 - это параметр для эллипсоидной области дренирования;
- это параметр для эллипсоидной области дренирования;
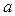 - половина большой оси эллипса дренирования в горизонтальной плоскости определяемая из выражения:
- половина большой оси эллипса дренирования в горизонтальной плоскости определяемая из выражения:
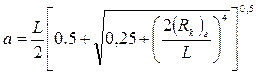 . (1.61)
. (1.61)
Среди многочисленных методов по определению дебита горизонтальной нефтяной скважины метод Joshi пригоден для расчета в диапазоне изменения длины горизонтального ствола 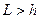 и
и 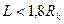 .
.
При выводе формул использовались следующие предположения:
· пласт считается изотропным;
· пластовая жидкость полагается вязкой, но несжимаемой;
· фильтрация пластовой жидкости подчиняется линейному закону Дарси;
· нефтяная залежь представляет собой круговой цилиндр высотой h с естественным режимом питания;
· режим фильтрации стационарный;
· пластовая жидкость характеризуется средними значениями вязкости;
· трение в скважине не учитывается.
В основе вывода формулы Борисова лежит полное фильтрационное сопротивление, которое можно представить суммой двух сопротивлений: внешнего – от контура питания до прямолинейной вертикальной галереи, совпадающей с проекциями горизонтальной скважины на кровлю (или подошву) пласта, и внутреннего, обусловленного тем, что мы имеем в действительности не галерею, а скважину.
В основе вывода формул (1.58)-(1.60) лежит замена трёхмерной фильтрации двумя плоскими задачами.
Влияние анизотропии пласта. В большинстве месторождений проницаемость в вертикальном направлении отличается от проницаемости в горизонтальном направлении. Различие вертикальной и горизонтальной проницаемости оценивается параметром анизотропии, то есть отношением горизонтальной проницаемости к вертикальной.
Для пласта с различной горизонтальной и вертикальной проницаемостями уравнение Лапласа, которое описывает установившийся режим фильтрации потока, имеет вид:
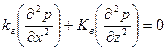 . (1.62)
. (1.62)
Это уравнение может быть представлено в виде:
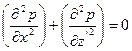 , (1.63)
, (1.63)
где
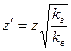 . (1.64)
. (1.64)
И эффективная проницаемость коллектора определяется как:
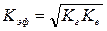 . (1.65)
. (1.65)
Таким образом, влияние анизотропии коллектора может быть учтено представлением толщины коллектора в виде:
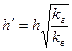 . (1.66)
. (1.66)
Решения установившегося состояния для горизонтальных скважин в уравнениях (1.57-1.60) представляют сумму двух математических решений, одно из которых – для горизонтального потока, а другое – для вертикального потока. Таким образом, можно изменить вертикальную составляющую уравнения установившегося состояния для учёта влияния анизотропии коллектора. После преобразований (1.57) получим уравнения Joshi (1.67) и (1.59) уравнение Борисова (1.68) с учетом влияния анизотропии:
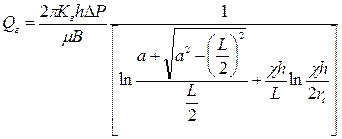 . (1.67)
. (1.67)
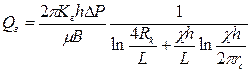 . (1.68)
. (1.68)
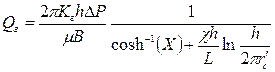 . 1.69)
. 1.69)
Коэффициент анизотропии 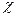 определяется из выражения:
определяется из выражения:
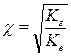 . (1.70)
. (1.70)
Приведенный радиус скважины 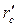 с учетом влияния анизотропии для метода Ренарда и Дюпии, определяется из выражения:
с учетом влияния анизотропии для метода Ренарда и Дюпии, определяется из выражения:
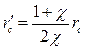 . (1.71)
. (1.71)
Метод Joshi пригоден для расчета в диапазоне изменения длины горизонтального ствола 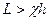 и
и 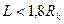 .
.
Дата добавления: 2017-04-05; просмотров: 3922;











