Линейный закон фильтрации Дарси

В 1856 г. французским инженером Дарси был установлен основной закон фильтрации, устанавливающий линейную связь между потерей напора Н₁ - Н₂ и объёмным расходом жидкости Q, текущей в трубке с площадью поперечного сечения F, заполненной пористой средой (рисунок 3.1).

Напор для несжимаемой жидкости запишется таким образом: 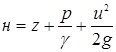, где z – высота положения;р/g – пьезометрическая высота; g есть объёмный вес; u– скорость движения жидкости.

Так как при фильтрации скорость обычно мала, то под напором понимается величина: 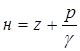. Закон Дарси имеет вид:

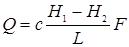, (3.3)

где с – коэффициент пропорциональности, называемый коэффициентом фильтрации и имеющий размерность скорости.

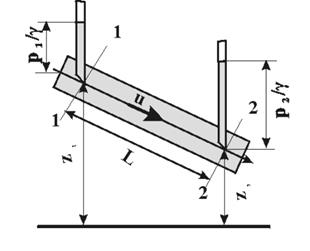
Рисунок 3.1 – Схема наклонного пласта

Закон Дарси показывает, что между потерей напора и расходом существует линейная связь. Запишем его в дифференциальной форме, учитывая соотношение:

u=Q/F,(3.4)

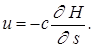
Или в векторной форме:

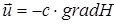, (3.5)

где s – расстояние вдоль оси криволинейной трубки тока.

Коэффициент фильтрации с характеризует среду и жидкость одновременно, т. е. зависит от размера частиц, от их формы и степени шероховатости, пористости среды, вязкости жидкости. Этот коэффициент обычно используется в гидротехнических расчетах, где приходится иметь дело с одной жидкостью – водой. При наличии различных жидкостей, что чаще бывает в подземной газонефтяной гидромеханике, использовать его неудобно. Поэтому закон Дарси записывается обычно в несколько ином виде:

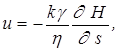
или

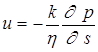, (3.6)

где h– коэффициент динамической вязкости; k– коэффициент проницаемости, характеризующий среду;р=g H – приведённое давление, равное истинному при z =0.

В системе СИ [k] = м². В смешанной системе, когда [p] = кГ/см², [h]=0,01г/см^.с=1спз, [s] = 1см, [u]= см/с, k измеряется в дарси.. Имеем:

.

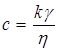Проницаемость песчаных коллекторов обычно находится в пределах k=100 – 1000 миллидарси, а для глин характерны значительно меньшие проницаемости.

Проницаемость определяется геометрической структурой пористой среды, т. е. размерами и формой частиц и системой их упаковки. Имеется множество попыток теоретически установить зависимость проницаемости от этих характеристик, исходя из закона Пуазейля для ламинарного движения в трубах и Стокса для обтекания частиц при той или иной схематизованной модели пористой среды. Поскольку реальные породы не укладываются в рамки этих геометрических моделей, то теоретические расчеты проницаемости ненадёжны. Поэтому обычно проницаемость определяют опытным путём.