Уравнения течения для пористой среды

Для нестационарного процесса при отсутствии источников и стоков имеем:

уравнение неразрывности:

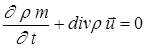; (4.1)

уравнение движения в форме Дарси:

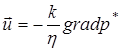, (4.2)

где р^*=р+zrg,r u=d G / dt,G – расход массы жидкости в единицу времени через поверхность равного потенциала (массовый дебит).

В приведённой системе уравнений k=const, h=const, т. е. среда изотропна. Для анизотропной среды слоистой структуры систему координат направляют по главным осям пласта, т. е. ось z – перпендикулярна слоям, а x, y – по плоскости слоя. В такой среде чаще рассматривают фильтрацию в предельных случаях. При k_z =0 – нет перетока газа через слои, а при k_z =¥имеемdp / dz =0, т. е. давление в каждом поперечном сечении распределяется гидростатически, а компоненты скорости, параллельные х, у, распределены равномерно по поперечному сечению потока.

При установившемся движении параметры потока (плотность, скорость фильтрации, пористость и т. д.) в каждой точке пористой среды постоянны и не зависят от времени. Таким образом, для установившейся фильтрации 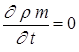и уравнение неразрывности примет вид :

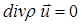, (4.3)

где 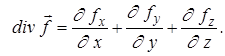(4.4)

Для несжимаемой жидкости (r=сonst) уравнение (4.3) запишется:

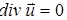. (4.5)