Закон фильтрации в трещиноватой среде
В трещиноватых пластах скорость фильтрации связана со средней скоростью через трещиноватость:
u=mтw.
Средняя скорость выражается через градиент давления по формуле Буссинеска при представлении течения по трещинам, как течения между двумя плоскими параллельными пластинами:
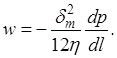
Используя последние зависимости, получим линейный закон фильтрации в трещиноватых средах:
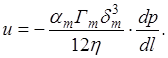 (3.8)
(3.8)
По аналогии с законом Дарси проницаемость трещиноватых сред равна:
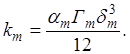 (3.9)
(3.9)
При рассмотрении трещинно-пористой среды как деформируемой, проницаемость трещинного пласта изменяется с изменением давления:
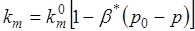 , (3.10)
, (3.10)
где 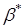 есть параметр зависящий от упругих свойств трещинной среды и геометрии трещин (см. формулу (2.4)).
есть параметр зависящий от упругих свойств трещинной среды и геометрии трещин (см. формулу (2.4)).
И в трещиноватых породах линейный закон может нарушаться при больших скоростях фильтрации из-за значительных по величине сил инерции. При этом значения критических чисел Рейнольдса зависят от шероховатости: для гладких трещин Reкр = 500, а для шероховатых до 0,4. Для шероховатых трещин выражение для числа Рейнольдса равно: 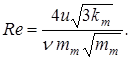
Дата добавления: 2017-06-13; просмотров: 1488;











