Определение неизвестной функции распределения(Л.4)

Сущность экспериментальной оценки характеристик качества состоит в том, что на основании полученных из опыта ограниченных исходных статистических данных производится определение фактических законов или возможных значений параметров с заданной точностью и достоверностью. При наличии известных аналитических связей между различными показателями качества элементов и систем в процессе эксперимента определяют те исходные показатели, получить которые проще и дешевле.

Так, например, при экспериментальной оценке надежности радиолокационного вооружения, являющейся одним из свойств качества, исходными статистическими данными обычно являются частные или суммарные реализации времени безотказной работы, времени восстановления и число отказов, возникших (и устраненных) за суммарное время. По этим исходным данным определяются неизвестные законы и параметры безотказности, восстанавливаемости, а также обобщенные показатели надежности с заданной точностью и достоверностью. Методы решения подобных задач рассмотрим на примере оценки неизвестных законов и параметров безотказности.

Основной характеристикой случайной величины является распределение плотности вероятности. Зная его, можно рассчитать все другие необходимые показатели. Рассмотрим решение задачи экспериментального определения неизвестной плотности вероятности F(t) случайной величины Т — времени безотказной работы некоторой радиоэлектронной системы. Определение плотности вероятности F(t) можно осуществить, если в качестве исходных данных будет известен достаточно большой объем статистики - п, частных конкретных реализаций Т= t, (i= 1, 2, 3,..., п) случайной величины Т.

Исходные значения величин Т — t₁ определяются следующим образом. Фиксируется начало испытаний системы на надежность после ее включения в работу. Отмечается момент возникновения первого отказа t₁. Первая величина T = t₁ будет равна интервалу времени с момента начала работы до момента возникновения первого отказа. Возникший отказ устраняется, и работа системы вновь восстанавливается. Новая случайная величина T = t₂ равна отрезку времени от момента второго включения до момента возникновения второго отказа и т. д. Таким образом, фиксируются все интервалы T=t₁ времени безотказной работы между двумя последовательными отказами. Для более достоверного определения F (t) необходимо продолжать испытания до тех пор, пока получится достаточно большое число реализаций n (п 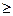100). Полученный набор всех величин T = t₁записывается в виде неупорядоченного статистического ряда (t_1,t₂,…t_i,…,t_n) или заносится в соответствующую таблицу.

Сформулируем задачу:

Дано: Набор n исходных статистических данных Т=t, (i=1, 2,...,n). Пусть n = 100.

Требуется определить аналитическую зависимость неизвестного закона F(t) — плотности вероятности случайной величины Т.

Решение. Определение неизвестного закона F(t) целесообразно производить в следующей последовательности:

A. Первичная обработка исходной статистики.

Б. Графическое изображение статистических данных.

B. Выравнивание статистических графиков.

Г. Определение критерия согласия.