В. Выравнивание статистических графиков

Неизвестная плотность вероятности F(t) является плавной и непрерывной кривой — функцией аргумента t. Гистограмма же 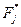хотя и напоминает по форме функцию F(t), имеет вид ступенчатой ломаной кривой (рис. 16). Если повторить аналогичный опыт по набору новой серии подобных случайных величин Т= t_i в тех же условиях эксперимента и для такой же системы, то построенная вновь гистограмма не совпадет с ранее полученной, хотя она по-прежнему будет напоминать неизвестную плотность F(t).

Рис.16 Гистограмма данных примера

Для того чтобы статистически согласовать гистограмму с плавной кривой F(t), производят статистическое выравнивание полученной ступенчатой кривой. Используя полученную гистограмму, производят соответствующий выбор некоторой функции 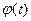, которая выравнивала бы гистограмму и с большой вероятностью приближалась бы по форме к неизвестной функции F(t). Другими словами, при выборе функции 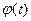требуется, чтобы она по вероятности совпадала с F(t), т. е.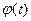 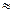F (t).

Статистическое выравнивание гистограммы производится в следующей последовательности:

—выбор одной из сглаживающих функций ,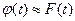

— расчет неизвестных параметров для выбранной сглаживающей функции;

— расчет теоретических значений сглаживающей функции в фиксированных точках t = t_j,

— построение графика сглаживающей функции;

— качественный вывод о справедливости допущения .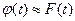

При выборе сглаживающей функции 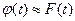стараются учесть особенности гистограммы и аналитическое выражение 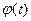, которое должно быть несложным и удобным в инженерных расчетах. Полезно учитывать особенности и опыт работы системы, для которой оценивается закон F(t).

Анализируя гистограмму, изображенную на рис.16, можно выбрать простую функцию 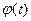в виде убывающей экспоненты, т. е.допустить, что

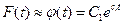16

При различных значениях параметров С₁ и С₂ имеется бесчисленное множество убывающих экспонент, среди которых надо выбрать только одну, обладающую свойствами плотности вероятности и особенностями полученной гистограммы. Следовательно, на выбираемую сглаживающую функцию (16) необходимо наложить определенные связи (требования). Число этих связей зависит от вида функции и количества, входящих в нее неизвестных параметров.

Первая связь, которую необходимо наложить на функцию 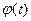за счет соответствующего подбора констант С₁ и С₂, называется нормирующим условием. Так как 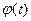должна быть плотностью вероятности и обладать нормирующим свойством, то необходимо выполнить первое условие: площадь под кривой в (t) должна быть равна единице, т. е.

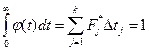17

Отсюда имеем

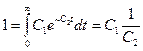
следовательно,

C₁ = C₂ = C

Значит, при выборе выравнивающей функции в виде убывающей экспоненты необходимо потребовать в первую очередь, чтобы эта экспонента зависела только от одного неизвестного параметра, т. е.

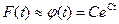18

Пока не наложено определенное условие на константу С, можно выбрать любое значение этой константы и при этом всегда будет выполнено нормирующее условие. Однако при произвольном значении константы 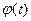будет плохо согласовываться с гистограммой.

Так как статистическая величина

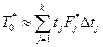
оценивает математическое ожидание T₀ случайной величины Т (т. е. То = М{Т}), то на выравнивающую функцию необходимо наложить вторую связь, а именно

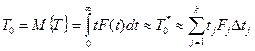19

Реализуя это условие, получим

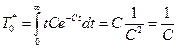, 20

Значит, величину параметра С нельзя брать произвольной, а необходимо ее рассчитывать из соотношения

.

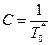Рассчитав по опытным данным величину 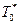(для нашего примера Т₀ = 50 ч), окончательно полагаем, что только функция 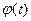вида

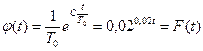21

будет согласовываться с данными эксперимента и обладать свойствами неизвестной плотности вероятности F(t).

Таким образом, наложив две связи на выравнивающую функцию (запомним число связей s = 2), полагаем, что неизвестная искомая плотность вероятности F(t) имеет вид

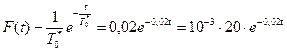22

Задаваясь теперь любыми фиксированными значениями Т=t_j, легко рассчитать теоретические значения F(t=t_j) и сравнивать их с опытными данными F_j*. График найденной функции F(t) обычно наносят на гистограмму и производят качественную оценку степени соответствия теоретического закона F(t) с опытными данными — гистограммой.

Так, например, анализируя графики гистограммы F_j* и расчетную кривую функции

F(t) =0,02е-^002t (рис.16 ), можно сделать качественный вывод о том, что выбранная F(t) неплохо согласуется с данными эксперимента.

Для того чтобы иметь не качественную, а количественную оценку степени соответствия выбранной F(t) статистическим данным, необходимо произвести численную проверку согласия.