Односторонние и двусторонние критерии

Если цель эксперимента состоит в установлении различия между двумя ГС, то знак этого не известен. На рис.15 представлена эта ситуация

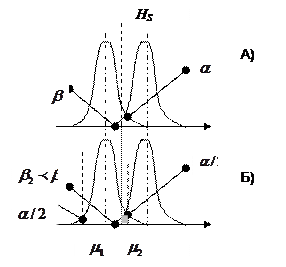
Рис.15. Односторонний и двусторонний критерий

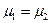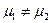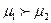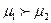. Когда нулевая гипотеза сформирована в виде Н₀: , то неизвестно какой из параметров имеет большее значение, тогда альтернативная гипотеза Н_А: , утверждает, что проверяемые значения относятся к разным совокупностям. Этот случай относится к понятию двустороннего критерия, так как Н_А , записанная в виде или рассматриваются как возможные исходы.

Если задано строгое условие типа Н₀: 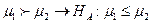или Н₀: 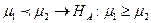, то такой критерий называется односторонним. Статистический критерий H_S определит ошибки первого и второго рода, как это показано на рисунке для случая 15 А). Если сохранить значение уровня значимости 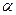неизменным, но сделать критерий двусторонним, то от хвостов распределения 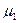отсекаются площади равные 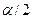(случай Б)). Видно, что при этом величина ошибки второго рода возрастает, как это представлено серой областью на рис 15 Б).

Значение ошибки второго рода зависит от объема выборки, от степени различия ГС

(расстояния между центрами распределений) и, наконец, от мощности критерия М= 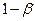. Следует запомнить, что односторонний критерий при одинаковых объемах выборки всегда мощнее двустороннего критерия!

Приведем главные правила оценки мощности критерия:

1. Критерий при заданной разнице между выборками тем мощнее, чем больше уровень значимости 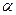и объем выборки n.

2.Если различие между средними значениями двух рассматриваемых выборочных распределений велико (хвосты распределений не пересекаются, то мощность критерия равна единице.

3.Если между распределениями практически нет различия, то отклонение верной гипотезы произойдет лишь в % случаев.