Распознавание статистических гипотез

При попарном сравнении двух образцов продукции или двух объектов экспертизы, полученных разными способами или на разных производствах, всегда встает вопрос, какой из них лучше. Сравнивать только средние значения нерационально, так как хвосты распределений могут наложиться друг на друга. При этом, решение принимается на основе статистических предположений (гипотез) о ГС с учетом разброса данных. Выбор правильного решения из двух противоположных предположений о ГС называется статистической проверкой гипотез. Информация при этом носит альтернативный характер, поэтому количественные оценки надо находить с помощью статистического оценивания.

Гипотеза о том, что две совокупности, с точки зрения одного или нескольких критериев, одинаковы, называется нуль - гипотезой - H₀. Поскольку критерии устанавливают только отличие совокупностей, H₀ выдвигается для проверки основания ее отбрасывания и принятия альтернативной гипотезы Н_А, указывающей, что расхождение между проверяемыми совокупностями есть. При проверке гипотез могут возникнуть два ошибочных решения: отклонение верной гипотезы с вероятностью 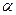и принятие неверной гипотезы с вероятностью 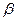. Подобный алгоритм представлен в таблице 9.

Таблица 9. Возможные исходы распознавания гипотез

	Ситуация
H0 верна	H0 не верна
Действие	Отвергнуть		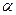1 -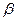
Принять	1 -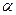

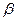
Вероятности, соответствующие, обеим исходам в литературе носят различные названия при сохранении начального смысла:

- Вероятность отклонения правильной H₀ гипотезы - ошибка первого рода 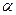, риск I, риск поставщика, риск излишней наладки технологического процесса и т.д.

- Вероятность неправильного принятия Н_А гипотезы - ошибка второго рода, риск II, риск потребителя или заказчика, риск незамеченной разладки технологического процесса и т.д.

Ошибки первого и второго рода уменьшаются при увеличении объема выборки и равны нулю при проверке ГС в целом. Ошибка первого рода принимается в пределах от 1 % до 10 %, ошибка второго рода от 10% и больше.

Приведем алгоритм распознавания гипотез на примере N- распределения, в случае проверки гипотез для других распределений алгоритм не меняется, а в нем используются статистики рассматриваемого распределения (см. таблицу 8).

1. Принимаем нулевую гипотезу H₀ : ( ),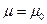

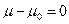2. Формируем альтернативную гипотезу HA : ( ),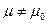

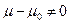3. Используем статистику N распределения 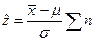или статистику любого другого проверяемого закона распределения

4. Принимаем уровень значимости 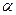и по нему из таблиц для проверяемого закона распределения находим табличное значение статистики z для принятого уровня значимости, такое, что при верной H0 соблюдалось условие .

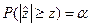5. Сравниваем статистическое и табличное значения статистик

если 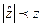, то Н0 не отвергается,

если 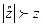, то Н0 отвергается на принятом уровне значимости .

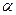Пример

Пусть взята первая выборка с параметрами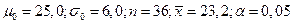

Н₀ :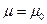

Н_А: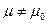

,

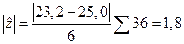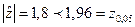, следовательно Н₀ подтверждается на принятом уровне значимости.

Пополним первую выборку до 49 членов, параметры выборки примут вид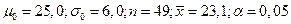

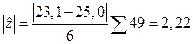
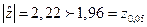, следовательно Н₀ отвергается на принятом уровне значимости.

В теории математической статистики рассматриваются разные виды критериев:

- критерии значимости ( принять или отклонить),

- параметрические критерии, когда проверяется численное значение параметра ,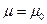

- критерии согласия, проверяющие согласуется ли экспериментальное распределение с гипотетическим распределением.