Г. Определение критерия согласия

Критерии согласия позволяют количественно обосновать приемлемость приближенного равенства

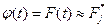23

Существует несколько критериев проверки согласия, но общую сущность их применения можно пояснить следующим образом:

а) выбирается мера расхождения 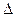между теоретической кривой F(t) и гистограммой F_j*. Эта мера расхождения может усредняться (или суммироваться) для всех выбранных значений интервалов 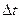или возможных значений изучаемой случайной величины Т.

Если мера расхождения А рассчитывается как модуль разности, например 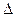= 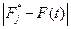, то чем меньше получится значение 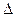, тем лучше согласие между F(t) и F_j* ,

б) назначается граничное допустимое значение меры расхождения 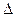= 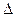_гр;

в) если опытное (расчетное) значение меры расхождения 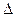= 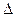_оп < 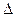_гр, то полагают, что выбранная функция F(t) хорошо согласуется с опытными данными. Если 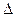_оп > 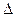_гр, то выбранное равенство (23) F(t) = F_j* отменяют или подвергают его большому сомнению.

Поскольку величина 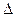зависит от случайных опытных значений F_j* , то она сама является случайной величиной и имеет свой вероятностный закон распределения. Этот закон определяется в соответствии с выбранным критерием согласия.

Допустим, что нам известна плотность вероятности 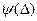случайной величины 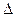[меры расхождения между F_j* и F(t)]. Пусть она имеет вид, изображенный на рис. 17.

Рис. 17 Зависимость распределения меры расхождения

При выборе допустимой меры расхождения 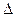_гр исходят из условия обеспечения достаточно большого значения вероятности неравенства 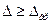т. е. требуют, чтобы

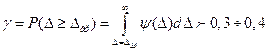. 24

Большое значение вероятности 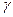эквивалентно тому, что опытное значение меры расхождения 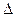= 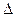_оп окажется меньше 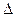_гр. Если, например, величина 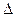_оп, рассчитанная по опытным данным, получилась близкой к нулю, то тогда заштрихованная площадь на рис. 17, численно равная вероятности

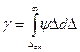
будет достаточно большой (близкой к единице). Значит, в этом случае с уверенностью, равной вероятности 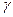, можно утверждать обоснованность хорошего согласия между выбранной функцией F(t) и опытными данными. Рассмотрим широко применяемый на практике критерий согласия хи-квадрат Пирсона.

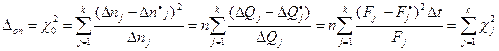25

При расчете опытного значения полученной меры расхождения 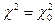, входящие в формулу 25 величины 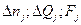рассчитываются по формулам:

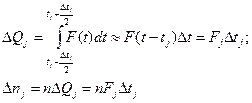26

Для нашего примера имеем:

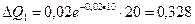
а опытное значение

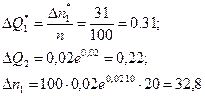
Значит, первое слагаемое суммы (25) будет равно.

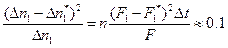
А второе

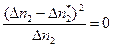
Плотность распределения 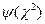случайной величины 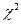зависит от параметра r, называемого числом степеней свободы распределения 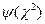. Число степеней свободы рассчитывается как разность r=k-s, где k — число интервалов (в нашем примере k = 8); s — число наложенных связей на функцию 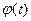(у нас s = 2).

Для некоторых значений чисел r рассчитаны таблицы значений вероятности неравенства 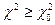на основе выражения:

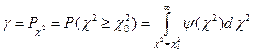27

Зависимость вероятности 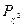от чисел r и 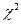берется из стандартных таблиц. Использование таблицы для применения критерия согласия хи-квадрат Пирсона сводится к следующему: по опытным и расчетным значениям 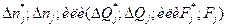рассчитывается опытное значение 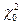по формуле (25).

Величина 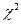по результатам расчета получилась равной 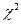=1,86; затем определяют число степеней свободы r (r=k—s = 8—2 = 6).

По входным данным 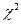= 1,86 и r = 6 из таблиц определяют, что вероятность 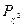>0,95.

Следовательно, полученная опытная мера расхождения 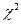=1,86 является малой (допустимой), при этом с уверенностью, численно равной вероятности 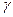= = 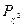95%, можно утверждать обоснованность и хорошее согласие приближенного вероятностного равенства (22)

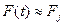
Таким образом, для нашего примера при расчетах можем полагать, что неизвестная плотность вероятности F(t) для исследуемой системы имеет вид

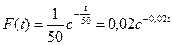
Приемлемое значение вероятности 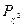должно лежать в пределах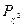 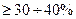. Если же полученная из таблицы вероятность 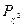окажется меньше 5—10%, то имеются все основания полагать, что выбранная плотность вероятности F(t) плохо согласуется с экспериментальными статистическими данными. В этом случае необходимо выбрать другую функцию F(t) и снова проверить ее по критерию согласия хи-квадрат Пирсона.