Задачи оптимизации при ограничениях в виде неравенств
Рассмотрим задачу поиска минимума функции
min f(x)
при условии
gi(x) £ 0, i = 1,2, …, k, x Î Rn.
Обозначим через D – область возможных значений аргументов функций gi(x). Если gi(x) = 0, то ограничение называется активным (насыщенным). Если gi(x) < 0, то ограничение называется неактивным (ненасыщенным)
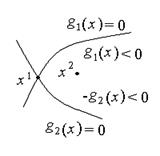
Рис. 4.1.
На рис. 4.1. отмечена точка x1, в которой оба ограничения являются активными. В точке x2 оба ограничения неактивные.
Предполагается, что в области D функции f(x) и gi(x) непрерывны и дифференцируемы по своим аргументам.
Предположим, что множество активных ограничений gi(x) = 0 равно m.
Для решения задачи оптимизации при ограничениях в виде неравенств, вводится функция Лагранжа вида
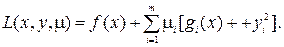 (4.1)
(4.1)
Необходимое условие экстремума можно записать в виде
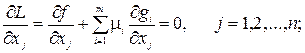 (4.2)
(4.2)
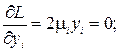 (4.3)
(4.3)
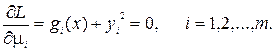 (4.4)
(4.4)
При решении этих уравнений надо придерживаться следующих правил. Из уравнения (4.3) следует, что возможны два варианта: 1) если mi = 0, то yi ¹ 0; 2) если yi = 0, то mi ¹ 0.
Если mi = 0, то функция Лагранжа равна f(x), решаем систему уравнений ¶f(x)/¶xj = 0, j = 1,2, …, n. Из полученных решений выделяем те, которые принадлежать области D. Вычисляем значения функции при этих решениях и запоминаем их. В этом случае мы находим стационарные точки соответствующие неактивным ограничениям. Вычисляем вторые частные производные, составляем матрицу Гесса и по критерию Сильвестра определяем точки локального минимума. Запоминаем эти точки и значения функций в этих точках.
Если mi ¹ 0, то согласно уравнению (4.3) yi = 0, и функция Лагранжа имеет такой же вид, как при решении задачи условного экстремума. Решая совместно уравнения (4.2) и (4.3) при yi =0, определяем условно стационарные точки x*. Вычисляем матрицу вторых производных от функции Лагранжа, и определяем ее положительную определенность в этих точках при выполнении условия 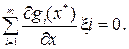 При выполнении этих условий в точке x* имеем локальный минимум. Запоминаем локальные минимумы при активных ограничениях, т.е. во внутренних точках области D.
При выполнении этих условий в точке x* имеем локальный минимум. Запоминаем локальные минимумы при активных ограничениях, т.е. во внутренних точках области D.
Сравнивая локальные минимумы внутри области D и на ее границе, выбирая среди них наименьшее значение, определяем минимум функции f(x) в области D.
Множители mI в выражении (4.1) называются множителями Куна-Такера. При yi равном нулю эти множители совпадают с множителями Лагранжа.
Приведенный метод дает последовательный алгоритм поиска экстремума при ограничениях в виде равенств и неравенств. Рассмотрим пример.
Пример.Надо определить минимум функции
f(x1, x2) = 3x12 + 2x22 - 3x1+1,
при условиях:
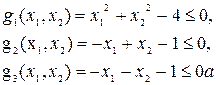
Границы областей ограничений представлены на рис. 4.2. Условие g1(x1, x2) = 0 определяет окружность с радиусом равным двум. При условии, что g2(x1, x2) = 0, имеем прямую, проходящую через точки A и B. Условие g3(x1, x2) = 0 определяет прямую, проходящую через точки A и C. Область D допустимых значений аргумента, в которой надо определить минимум функции, находится внутри границы, обозначенной на рис.4.2 через ABECA.
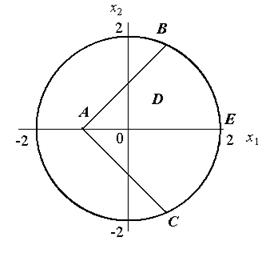
Рис. 4.2.
Составляем функцию Лагранжа
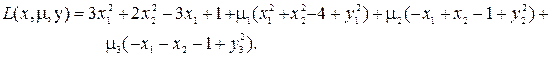
Вычисляем производные по всем аргументам и приравняем их нулю:
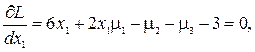
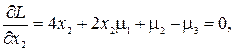
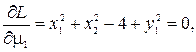 (4.5)
(4.5)
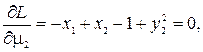
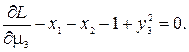
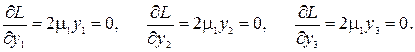
В результате получили восемь нелинейных уравнений с восемью неизвестными.
а) Приравняем нулю все множители Куна-Такера: m1 = 0, m2 = 0, m3 = 0. В этом случае найдем точку безусловного экстремума и определим принадлежность ее области D.
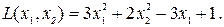
Определяем частные производные
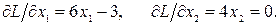
Вычисляем стационарную точку x0 = (0.5 0)T и значение функции в этой точке f(0.5, 0) = 0.25. Эта точка принадлежит области D.
Если приравнять одновременно нулю y1 = y2 = y3, и решать систему уравнений, то получим множество решений относительно переменных x1, x2, m1, m2, m3 . Эти решения лежат на окружности или принадлежат отрезкам AB, AC Аналитически решить эту систему, применяя методы компьютерной алгебры [Mathcad MATLAB], не удается. Поэтому поступим следующим образом.
б) Положим m1 ¹0, m2 = m3 =0. Это означает, что ограничение g1(x1, x2) является активным, а остальные два ограничения g2(x1, x2), g3(x1, x2) выполняются. В этом случае отыскиваем минимум на дуге BEC. Имеем
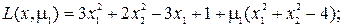
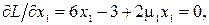
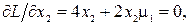
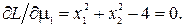
Решая эту систему из трех уравнений, получаем два решения: 1) x1(1) = 1.5, x2(1) = 1.323, m1(1) = -2; 2) x1(2) = 1.5, x2(2) = -1.323, m1(2) = -2. Эти точки x(1) и x(2) лежат на дуге BEC. Значение функции в этих точках f(1.5,1.323) = f(1.5, -1.323) = 6.75. Квадратичная форма от матрицы вторых производных 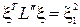 и положительно определена. Значит в точках x(1) и x(2) имеем относительный минимум. С другой стороны, функция f(x1,x2) является выпуклой в выпуклой области D, поэтому условия равенства нулю частных производных первого порядка являются достаточными для существования относительного минимума.
и положительно определена. Значит в точках x(1) и x(2) имеем относительный минимум. С другой стороны, функция f(x1,x2) является выпуклой в выпуклой области D, поэтому условия равенства нулю частных производных первого порядка являются достаточными для существования относительного минимума.
в) Ищем минимум функции на отрезке AB, где выполнено условие g2(x1, x2) = 0. Для этого случая положим m2 ¹ 0, m1 = m3 =0. Записываем функцию Лагранжа и ее частные производные приравняем нулю:
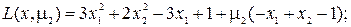
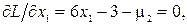
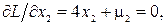
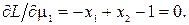
Решая эту систему уравнений, найдем x1(3) = -0.1, x2(3) = 0.9, m2 = -3.6. Точка x(3) = (-1, 0.9) принадлежит отрезку AB. Из уравнения связи 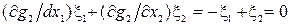 имеем, что x1 = x2. Квадратичная форма от матрицы вторых производных
имеем, что x1 = x2. Квадратичная форма от матрицы вторых производных 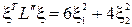 положительна. В точке x(3) = (-0.1, 0.9) имеем локальный минимум искомой функции равный f(-0.1, 0.9) = 2.95.
положительна. В точке x(3) = (-0.1, 0.9) имеем локальный минимум искомой функции равный f(-0.1, 0.9) = 2.95.
г) Определим минимум функции на отрезке AC, где g3(x1, x2) = 0. Для этого случая положим m3 ¹ 0, m1 = m2 =0. Записываем функцию Лагранжа, и ее частные производные приравняем нулю:
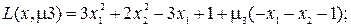
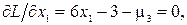
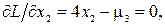
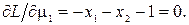
Решая эту систему уравнений, найдем x1 = -0.1, x2 = -0.9, m2 = -3.6. Точка с координатами (-1, -0.9) принадлежит отрезку AС. Из уравнения связи 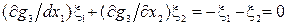 имеем, что x1 = -x2. Квадратичная форма от матрицы вторых производных
имеем, что x1 = -x2. Квадратичная форма от матрицы вторых производных 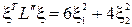 положительна, и в точке с координатами x(4) = (-0.1, -0.9) имеем локальный минимум искомой функции на отрезке AC равный f(-0.1, -0.9) = 2.95.
положительна, и в точке с координатами x(4) = (-0.1, -0.9) имеем локальный минимум искомой функции на отрезке AC равный f(-0.1, -0.9) = 2.95.
В результате нашли четыре точки локального экстремума, принадлежащих области D. Среди них в точке x(0) = (0.5, 0) исследуемая функция имеет наименьшее значение f(0.5, 0) = 0.25.
На данном примере рассмотрели процедуру решения задачи оптимизации при ограничениях в виде неравенств. Эта задача сложнее, чем задача поиска безусловного и условного экстремумов.
В заключении отметим, что задача поиска экстремума сводится к решению нелинейных систем уравнений. Найти аналитическое решение систем уравнений возможно только в некоторых частных случаях. Разработаны различные способы приближенного решения таких уравнений. Применение этих способов сводится к тому, что задаются точка начального приближения x* = (x1*,x2*, …, xn*). Далее строится некоторая последовательность точек {xk}. При условии, что эта последовательность сходится к решению систем уравнений, можно найти искомое решение. Условие сходимости зависит от используемого способа численного решения, от свойств целевой функции и от начального приближения, которое задается лицом, решающим систему уравнений. Универсальной методики задания начального приближения, обеспечивающего сходимость решения, не существует. В каждом случае надо использовать различные способы анализа: свойства выпуклости целевой функции, пределы изменения ее частных производных, линейность некоторых уравнений системы и т.д.
Дата добавления: 2021-07-22; просмотров: 508;











