Относительный экстремум. Метод множителей Лагранжа

1. Метод исключения. Рассмотрим теперь задачу на относительный экстремум. Как мы видели, решение задачи об отыскании экстремумов функции п переменных f(x) на всем пространстве Е_п может быть сведено с помощью необходимых условий к решению системы уравнений (2.1), в результате чего определяются стационарные точки функции f(х). Оказывается, что аналогичное сведение к решению уравнений возможно и для задачи отыскания экстремумов функции f(x) при наличии ограничений типа равенств

(3.1)

g_i (x) = 0, i = l, 2, ..., m.

Условия (3.1) принято называть уравнениями связи.

Уточним, что именно мы будем понимать под решением задачи на относительный экстремум. Точку х, удовлетворяющую условиям (3.1), мы будем назвать допустимой.

Определение 3.1. Допустимая точка x⁰доставляет относительный локальный минимум функции f(x), если можно указать такое число ε > 0, что для всех х, удовлетворяющих уравнениям связи (3.1) и условию ||х – x⁰|| < ε, имеет место неравенство

f ( x ) ≥ f (x⁰).

Рассмотрим случай, когда уравнения связи (3.1) могут быть разрешены относительно части переменных. Будем предполагать, что функции g_i(х), i = l , ... , m, имеют в окрестности рассматриваемой допустимой точки x⁰ непрерывные частные производные по всем аргументам до второго порядка включительно и, кроме того, ранг матрицы Якоби для функций g_i(х), i = l , ..., m, рассматриваемой в точкеx⁰, равен т. Не нарушая общности, предположим, что отличен от нуля определитель (якобиан), составленный из частных производных по первым т аргументам, т. е.

(3.2)

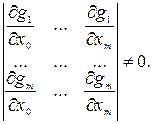
Тогда по теореме о неявных функциях в некоторой окрестности точки x⁰система уравнений (3.1) разрешима относительно х₁, ..., х_m, т. е. представима в виде

(3.3)

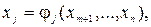j = 1, 2, … , m ,

где 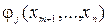— непрерывно дифференцируемые в рассматриваемой окрестности функции. Переменные x₁ ..., х_m естественно назвать «зависимыми», в отличие от «независимых» — x_m+1, ..., х_n. Подставляя выражения (3.3) в функцию f(x), получим задачу отыскания безусловного экстремума функции п-т переменных

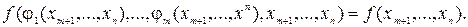
Однако провести исключение части компонент вектора х обычно бывает трудно или даже невозможно. Поэтому мы используем другой путь определения точки x⁰, который не предполагает наличия явных выражений типа (2.3), хотя использует существенно условие (2.2).

2. Метод множителей Лагранжа. Как мы видели в замечании к теореме 1.1, в точке x⁰, доставляющей безусловный экстремум функции, ее полный дифференциал равен нулю, т. е.

(3.4)

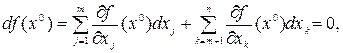
где dx_j, j = 1, ..., m, — дифференциалы «зависимых» переменных, связанные с дифференциалами «независимых» переменных dx_k, k = m+1,..., п, следующим образом:

(3.5)

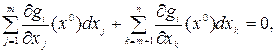i = 1, 2, … , m

Уравнения (3.5) получены при дифференцировании полным образом уравнений связи (3.1). Исключим теперь дифференциалы «зависимых» переменных из уравнений (3.4), (3.5). Для этого умножим каждое из уравнений системы (3.5) на произвольные множители 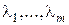и результаты сложим с уравнением (3.4), тогда получим следующее равенство:

(3.6)

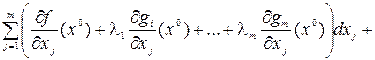
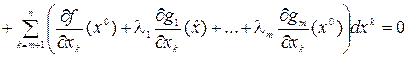
Распорядимся множителями 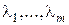таким образом, чтобы обратились в нуль коэффициенты при дифференциалах «зависимых» переменных, т. е.

(3.7)

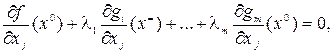j = 1, 2, … , m

Это можно сделать, так как уравнения (2.7) являются системой линейных алгебраических уравнений относительно множителей 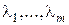которая имеет единственное решение в силу того, что ее определитель (3.2) по условию отличен от нуля. При выбранных таким образом значениях множителей в равенстве (3.6) останутся только члены, содержащие дифференциалы «независимых» переменных. Поэтому коэффициенты при этих дифференциалах должны быть нулями, т. е.

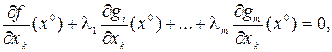k = m + 1, … , n . (3.8)

Таким образом, мы получили систему п + т уравнений (3.1), (3.7), (3.8) относительно п + т неизвестных x₁⁰,...,x_n⁰, 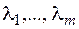. Этот результат представляет собой основное содержание метода множителей Лагранжа и позволяет определить множество «претендентов» на решение в задаче на относительный экстремум. Метод Лагранжа состоит из следующих этапов:

1) составляется функция п + т переменных, которая называется функцией Лагранжа:

(3.9)

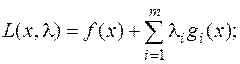
2) вычисляются и приравниваются нулю ее частные производные по х и :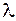

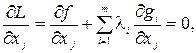(3.10)

j = 1, … , n ,

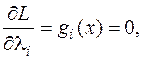i = 1, … , m ;

3) решается система (3.10) п + т уравнений относительно п + т неизвестных x₁,..., x_n, .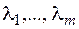

Система уравнений (3.10) представляет собой необходимые условия первого порядка в задаче на относительный экстремум, а ее решения x₁⁰, ..., x_n⁰ принято называть условно-стационарными точками. Как и в случае задач на безусловный экстремум, необходимые условия первого порядка не определяют характера условно-стационарной точки. Для выяснения этого вопроса следует привлечь производные более высоких порядков функций f(х)и g(x).

Заметим, что требование неравенства нулю якобиана (3.2) является существенным. Только в этом случае система уравнений (3.7) разрешима, причем единственным образом, относительно множителей Лагранжаl₁, l₂, …, l_m.

3. Пример. Условие (3.2) может быть не выполнено, если решение задачи на относительный экстремум реализуется, например, в точке касания поверхностей ограничений (3.1). Пусть

n = 2, m = 2, f(x) = x₂,

g₁(x) = (x₁ – 1)² + (x₂)² – 1,

g₂(x) = (x₁ – 1)² + (x₂)² – 1.

Допустимая точка должна одновременно удовлетворять уравнениям g₁(x) = 0, g₂(x) = 0 и является единственной: x₁ = 0, х₂ = 0. Очевидно, что точка x₁= 0, x₂ = 0 и будет решением задачи на относительный минимум функции f(х)= х₂при ограничениях g_l(х)= g₂(х)= 0. Составим для этой задачи функцию Лагранжа:

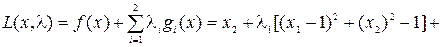
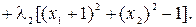
Метод множителей Лагранжа приводит к уравнениям

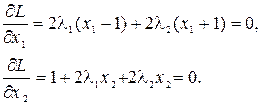
Этим уравнениям точка относительного минимума x₁ = 0, x₂ = 0 не удовлетворяет ни при каких значениях 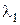, , 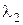т. е. в данном случае метод множителей Лагранжа не работает.

Заметим попутно, что метод множителей Лагранжа можно применять всегда для функции Лагранжа более общего вида

(3.11)

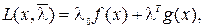
причем приведенному примеру соответствует система множителей Лагранжа 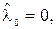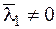, 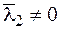. В случае же, когда выполнено условие (3.2), мы получаем единственную систему множителей Лагранжа с 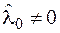. Поэтому все множители можно разделить на 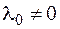и пользоваться функцией Лагранжа в виде (3.9).