Принцип максимума Понтрягина

Рассмотрим принцип максимума Понтрягина. При отсутствии фазового ограничения (3.4) и наличии ограничения на управлении в виде включения uÎU, где U – допустимоемножество значений управления, можно сформулировать следующую задачу Лагранжа:

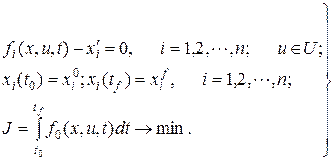(3.14)

Составляется функция Лагранжа:

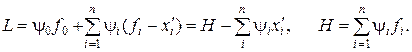(3.15)

В соответствии с приемом Лагранжа задача (3.14) сводится к задаче

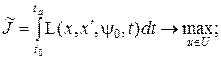(3.15)

при тех же граничных условиях для x(t) из выражения (3.14). Ищется максимум функционала 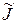, хотя в исходной задаче функционал J требуются минимизировать, так как в неособом случае принято, что множитель 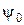= -1.

Идея принципа максимума заключается в том, что решение одной задачи (3.15) сводится к решению двух задач:

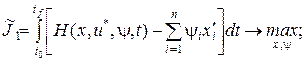(3.16)

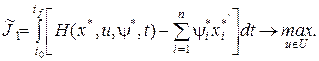(3.17)

при тех же граничных условиях, что в задаче (3.15).

Задача (3.15) простейшая задача вариационного исчисления. Для нее необходимые условия (уравнения Эйлера) имеют вид

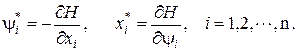(3.18)

В задаче (3.17) управление u^*(t) доставляет максимум в том и только в том случае, если всюду на [t₀, t_f], кроме точек разрыва u^*(t), выполнено равенство

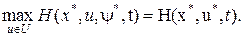(3.19)

П р и н ц и п м а к с и м у м а П о н т р я г и н а.Для того чтобы допустимая для задачи (3.14) пара (u^*(t), x*(t)) была ее решением, необходимо, чтобы существовали константа y₀^* < 0 и решение y^*(t)= (y₁^*, …, y_n^*)^T сопряженной системы (3.18) при x(t) = x^*(t) и u(t) = u^*(t), что при любом t Î [t₀, t], кроме точек разрыва u^*(t), функция H(x^*, u, y^*, t) достигает при u(t) = u^*(t) максимума, т.е. выполняется соотношение (3.19).

Принцип максимума Понтрягина применяется для синтеза оптимального программного управления в виде функции времени, т.е. для систем разомкнутого управления.