Управляемость и наблюдаемость. Наблюдатели

Для решения задач управления важно знать, обладает ли объект свойством управляемости. Если система не управляема, то нет смысла ставить и решать задачи проектирования оптимальных систем управления. Понятия управляемости и наблюдаемости были введены американским ученым Р.Калманом.

Пусть уравнение объекта имеет вид

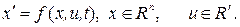(4.1)

Определение управляемости. Объект называется управляемым, если можно найти такое управляющее воздействие, позволяющее перевести объект из состояния x(t₀) в состояние x(t_f).

Рассмотрим линейную систему

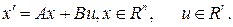(4.2)

Введем матрицу управляемости

У = [A AB A²B … A^n-1B]. (4.3)

Линейный стационарный объект (4.2) управляем тогда и только тогда, когда ранг матрицы управляемости равен n, где n – порядок системы (4.2).

Пусть объект описывается уравнениями состояния и выхода

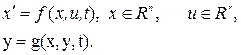(4.4)

Определение наблюдаемости. Система (1), (3) называется наблюдаемой, если по данным измерения выходного y(t) и управляющего сигналов u(t) на определенном промежутке времени t Î [t₀, t_k] можно определить переменные состояния x_i(t), i = 1,2, …, n.

Рассмотрим линейную систему

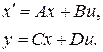(4.4)

Введем матрицу наблюдаемости системы (4.4)

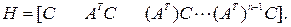(4.5)

Линейная стационарная система (4.4) наблюдаема, наблюдаема тогда и только тогда, когда ранг матрицы наблюдаемости равен n.

Для линейных стационарных систем справедлив принцип двойственности. Рассмотрим наряду с системой

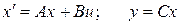(4.6)

двойственную (дуальную) ей систему

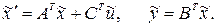(4.7)

Имеет место следующий принцип двойственности (дуальности): система (4.6) наблюдаема тогда и только тогда, когда двойственная ей система (4.7) управляема, и система (4.6) управляема тогда и только тогда, когда двойственная ей система (4.7) наблюдаема.

Отметим, что свойство двойственности (дуальности) используется при проектировании наблюдателей Калмана. Наблюдатели применяются для восстановления переменных состояния x(t) по измерениям входных и управляющих сигналов.