Метод множителей Лагранжа
Два первых метода основаны на простейшей задаче вариационного исчисления: найти экстремум функционала
 (3.1)
(3.1)
Функция, которая доставляет экстремум функционалу, должна удовлетворять уравнению Эйлера
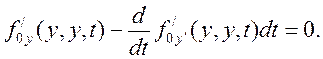 (3.2)
(3.2)
В том случае, когда функция является функцией многих переменных f(y1,y2, …,yn,t), то вместо одного уравнения (3.2) получится система дифференциальных уравнений, которые имеют вид (3.2) для каждой из переменных.
Рассмотрим задачу оптимального управления:
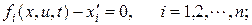 (3.3)
(3.3)
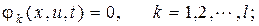 ( 3.4)
( 3.4)
 (3.5)
(3.5)
 (3.6)
(3.6)
где уравнения (3.3) – уравнения объекта управления, (3.4) – ограничения на аргументы x и u функционала J, (3.5) – граничные условия, (3.6) – критерий оптимальности. Эта задача оптимального управления называется задачей Лагранжа с закрепленными концами и фиксированным временем.
Составляется функция Лагранжа
 (3.7)
(3.7)
где yi – функции времени, lk , y0 – постоянные, которые называются множителями Лагранжа. Прием Лагранжа состоит в том, что задача (3.3) – (3.6) преобразуется в простейшую задачу вариационного исчисления для интегрального выражения
 (3.8)
(3.8)
В преобразованной задаче роль независимого аргумента играет вектор y = (x, u, l, y), а роль подынтегральной функции – функция Лагранжа. Тогда по аналогии с простейшей задачей вариационного исчисления, с учетом того, что в функцию Лагранжа не входит производные функций u, l, y, уравнения Эйлера-Лагранжа принимают вид
 (3.9)
(3.9)
Уравнения Эйлера-Лагранжа записывают, также используя Гамильтона
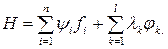 (3.10)
(3.10)
Тогда функция Лагранжа имеет вид
 (3.10)
(3.10)
и из уравнений (3.9) с учетом функции Гамильтона получаем
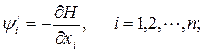 (3.11)
(3.11)
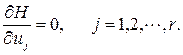 (3.12)
(3.12)
Правило множителей Лагранжа: если допустимая пара (u(t), x(t)) является решением задачи оптимального управления (3.3) - (3.6), то найдутся такие не равные одновременно нулю множители Лагранжа, что эта пара удовлетворяет уравнениям Эйлера-Лагранжа (3.11).
Согласно этому правилу, чтобы найти оптимальное управление и оптимальную траекторию, надо решить совместно уравнения (3.3), (3.4), (3.11), (3.12) при краевых условиях (3.5). Для определения 2n+r+l неизвестных xi (i = 1,2, … , n), yi (i = 1,2, …, n), uj (j = 1,2, …, r), lk (k = 1,2, …, l) имеется столько же уравнений. Среди них имеются 2n дифференциальных уравнений (3.3) и (3.11), при решении которых можно использовать 2n краевых условия (3.5). Уравнения (3.4) и (3.12) являются функциональными. При решении практических задач вызывают трудности решение дифференциальных уравнений с краевыми условиями. В системе MATLAB можно получить аналитическое решение линейных стационарных дифференциальных уравнений. Это обстоятельство существенно облегчает задачу синтеза оптимальных алгоритмов управления линейных стационарных систем.
Множители Лагранжа входят в уравнения Эйлера-Лагранжа линейно и однородно. Поэтому они определяются с точностью до постоянного множителя. Поэтому один из множителей Лагранжа можно приравнять числу, отличному от нуля. Условились в неособом случае (y0 ¹ 0) принимать y0 = -1.
Применяя метод множителей Лагранжа, определяют управление как функции времени, т.е. проводится синтез алгоритма разомкнутого управления.
Во многих прикладных задачах на управление накладывается ограничение типа неравенства. Часто оптимальное управление в таких задачах имеет разрыв. Метод множителей Лагранжа не позволяет определить число и местоположение точек разрыва, и поэтому в этих случаях он не позволяет находить оптимальное управление. Такие задачи эффективно решаются с помощью максимума Понтрягина, сформулированный академиком Л.С. Понтрягиным в 1953 году.
Дата добавления: 2021-07-22; просмотров: 493;











