Метод динамического программирования

Метод динамического проектирования (ДП) позволяет проектировать замкнутые оптимальные системы. Основу динамического программирования как метода оптимизации составляют: 1) принцип оптимальности; 2) инвариантное погружение, т. е. включение исходной задачи в семейство аналогичных задач; 3) функциональное уравнение, полученное на основе принципа оптимальности и инвариантного погружения.

Основная идея метода состоит в том, что вместо решения исходной задачи ее включают в некоторое семейство задач оптимизации (инвариантное погружение). При этом может оказаться, между отдельными задачами существуют простые соотношения и среди задач семейства найдется такая, которая легко решается. Тогда используя решение последней и соотношения, связывающие отдельные задачи семейства, получаем решение исходной задачи.

Рассмотрим следующую задачу.

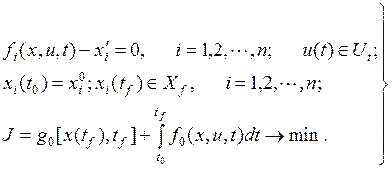(3.20)

Принцип оптимальности для этой задачи формулируется так: для оптимальности допустимой для (3.20) пары (u(t), x(t))необходимо, чтобы при любом t^’Î[t₀, t_f] управление u^*[t^', t_f] было оптимальным относительно состояния x^*(t^’), в котором окажется объект в момент t^’при использовании на начальном отрезке времени t₀ £ t < t^’ управления u[t₀, t^’]. Это прямой принцип оптимальности. В обратном принципе оптимальности за первоначальный берется отрезок [t^’, t_f], а управление на отрезке [t₀, t^’] должно быть оптимальным относительно состояния x(t^’).

Вводится функция Беллмана для задачи (3.20)

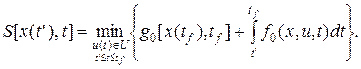(3.21)

Для этой функции выполняется условие S(x(t_f), t_f) = g(x(t_f), t_f). Решение задачи (3.20) сводится к уравнению Беллмана

(3.21)

Эти уравнения дают необходимые условия минимума. Если правые части уравнений объекта и подынтегральное выражение в критерии оптимальности явно не зависят от времени, то ¶S/dt = 0.

Достоинством метода динамического программирования является то, что этот метод позволяет находить оптимальное управление как функцию фазовых координат, т.е. позволяет решать задачу синтеза оптимального регулятора. В этом случае оптимальная система будет замкнутой. Недостатком метода является необходимость решения нелинейного уравнения в частных производных, что представляет большие трудности.