Экстремум функции многих переменных

Рассмотрим задачу поиска экстремума функции многих переменных

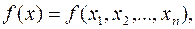(2.1)

где x Î Rⁿ – n-мерный вектор.

Напомним, что совокупность всех n-мерных векторов, для которых введены операции сложения, вычитания, умножение на число, скалярного произведения называют n-мерным вещественным евклидовым пространством. R¹ – это множество вещественных чисел, R² – двухмерное множество на плоскости, R³ – множество представляет собой трехмерную поверхность.

Скалярное произведение векторов записывают в виде

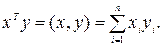(2.2)

Нормой (длиной) вектора называют число

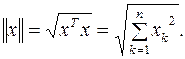(2.2)

Расстояние между точками x и y вычисляется по формуле

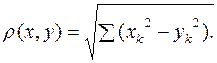(2.3)

1. Необходимое условие безусловного экстремума. Рассмотрим задачу безусловной минимизации скалярной функции f (x) векторного аргумента x размерности n, т. е. x = Rⁿ.

Необходимое условие безусловного экстремума следует из следующей теоремы.

Теорема 2.1. Для того чтобы в точке x⁰ функция f (x¹, ... , хⁿ) имела безусловный локальный экстремум, необходимо, чтобы все ее частные производные в этой точке должны быть равны нулю:

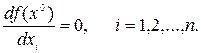(2.4)

Доказательство. Пусть в точке x⁰ функция f(x) достигает минимума. Зафиксируем все аргументы функции f(x), кроме одной x_j. Получим функцию одной переменной x_j:

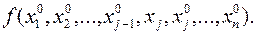
Для функции одной переменной, согласно необходимым условиям экстремума функции одной переменной теоремы 1.2, в точке экстремума производная по x_j равна нулю:

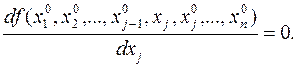
Проведя аналогичные рассуждения относительно для переменных x_j (j=1, 2, …,n) убеждаемся, что в точке экстремума все частные производные функции f(x) равны нулю. Теорема доказана.

Точки, в которых выполнено необходимое условие экстремума, называются стационарными.

Условие стационарности записывается в одной из следующих эквивалентных форм:

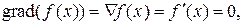
где 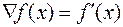-n-мерный вектор с компонентами 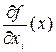, i=1, ..., n, который называется градиентом функции f (x) в точке x.

Из курса математического анализа известно, что градиент функции, как вектор, определяет направление возрастания функции, а антиградиент 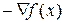– направление убывания функции.

Заметим, что необходимое условие экстремума (2.4) эквивалентно равенству нулю дифференциала функции f (x): df(x) = 0. В самом деле, если выполнено условие (2.4), то для любых dx_i, i = l, ..., п, имеем

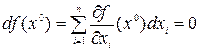
Справедливо и обратное утверждение, так как из последнего равенства в силу произвольности независимых приращений dx_i, i = 1, ..., п, следует, что все частные производные в точке x⁰равны нулю:

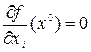, i = l, ..., п

Условия (2.4) образуют систему п уравнений для определения п компонент вектора x. Эти уравнения могут иметь различную природу и допускать любое количество решений, в частности, не иметь ни одного. Как и выше, точки x⁰, являющиеся решениями системы уравнений (2.4), будем называть стационарными, а условие (2.4) — необходимым условием экстремума первого порядка.

Система уравнений (2.4) в общем случае нелинейные, и самая основная проблема методов оптимизации – поиск решения этой системы уравнений. Системы Mathematica, MATLAB, Mathcad, Maple имеют программы для аналитического и численного решения нелинейных систем уравнений. Проблема заключается в том, что не для всех систем уравнений можно найти аналитические решения в виде комбинации элементарных функций. Численные методы решения не всегда сходятся к истинному решению. Сходимость решения зависит от задания значения начального приближения. Основная проблема заключается в следующем – как надо задать такое начальное приближение, чтобы последовательность значений сходилось к решению системы. Различные методы численного решения систем уравнений отличаются друг от друга разными скоростями сходимости и используют различные порядки производных минимизируемой функции. Численные методы поиска экстремума будут рассмотрены в дальнейшем.

2. Достаточные условия экстремума функции многих переменных. После того как решение x⁰системы уравнений (1.1) будет найдено, необходимо еще определить характер стационарной точки. Для этого нужно исследовать поведение функции f(x)в окрестности стационарной точки x⁰. Снова воспользуемся разложением функции f(х)в ряд Тейлора, предполагая ее дважды непрерывно дифференцируемой по всем переменным х₁,... , х_n. Тогда получим

(2.5)

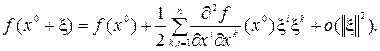
Здесь через 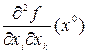обозначены элементы матрицы вторых производных функции f(x) в стационарной точке x⁰, а через 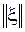—норму вектора 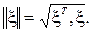. Матрица вторых производных, которую также называют гессиан, имеет вид

(2.6)

.

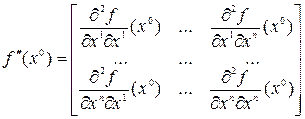Характер стационарной точки x⁰ функции f(x) связан со знакоопределенностью квадратичной формы

(2.7)

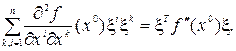
Квадратичная форма называется положительно определенной, если

(2.8)

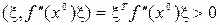
для любых векторов 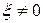. Здесь также приведен другой вид записи квадратичной формы с использованием скалярного произведения.

Соответственно, симметричная матрица вторых производных f"(x⁰)называется положительно определенной, если выполнено (2.8). Отрицательно определенным квадратичным формам и матрицам соответствуют противоположные знаки в неравенстве (2.8).

Таким образом, с учетом разложения (2.5), приходим к следующей формулировке условий второго порядка экстремальности функции f(x¹,..., х^п).

Теорема 2.2. Для того чтобы дважды непрерывно дифференцируемая функция п переменных f (x) имела в стационарной точке x⁰ безусловный локальный минимум (максимум), достаточно, чтобы матрица ее вторых производных была положительно (отрицательно) определенной.

3. Условия знакоопределенности квадратичных форм и матриц. Критерий Сильвестра. Проверка знакоопределенности матриц может быть осуществлена, например, с помощью критерия Сильвестра. Согласно этому критерию, необходимым и достаточным условием положительной определенности квадратичной формы (х^T Ах), где А = {a_ij}— симметричная п 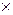п матрица, является выполнение п неравенств:

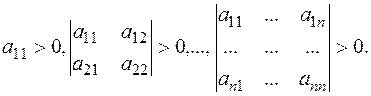
Необходимым и достаточным условием отрицательной определенности квадратичной формы (х, Ах)является выполнение цепочки следующих п неравенств:

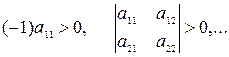
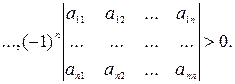
Если квадратичная форма не меняет знака, но обращается в нуль при ненулевых значениях аргумента, то для определения характера cстационарной точки x⁰требуется исследование производных более высокого порядка.

4. Пример. Проиллюстрируем содержание настоящего параграфа на следующей задаче: определить экстремальные значения функции

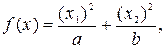
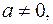
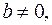
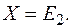
Из необходимых условий (2.4) имеем

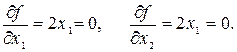
Поэтому x₁ = 0, x₂ = 0 стационарная точка. Коэффициенты квадратичной формы (2.5), вычисленные в ней, равны

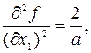
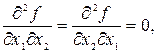
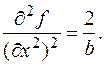
Тогда, согласно теореме 2.2, имеем следующие случаи:

1) 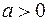, 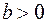— функция f(x) имеет в точке x⁰= (0, 0)^T минимум;

2) 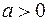, 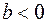— экстремума нет;

3) 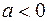, 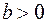— экстремума нет;

4) 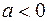, 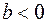— функция f(х)имеет в точке x⁰= {0, 0}^T максимум.

Отметим, что случаи 1) и 4) соответствуют поверхности, являющейся эллиптическим параболоидом, а случаи 2) и 3) — гиперболическому параболоиду, имеющему стационарную точку типа «седло».